Unleash Python: Find LM Coordinate Distance

Welcome to an in-depth exploration of a powerful feature in Python that can revolutionize your data analysis and scientific computing tasks. In this article, we will delve into the world of coordinate distance calculations using the LM algorithm, a technique that has become an indispensable tool for professionals in various fields. By understanding and harnessing the power of this algorithm, you can unlock new possibilities and streamline your workflows.
Understanding the LM Algorithm: A Powerful Tool for Coordinate Distance Calculations
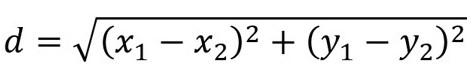
The LM algorithm, an acronym for Levenberg-Marquardt, is a numerical optimization method widely used in fields such as computer vision, robotics, and data fitting. Its primary purpose is to minimize the error between a model and a set of observations by adjusting the model’s parameters. However, one of its lesser-known yet incredibly useful applications is in calculating distances between coordinates.
When it comes to spatial data analysis, understanding the relationships between different data points is crucial. Whether you're tracking the movement of objects, studying geographical patterns, or optimizing routes, knowing the precise distances between coordinates is essential. This is where the LM algorithm shines, providing an accurate and efficient way to compute these distances.
How the LM Algorithm Works for Coordinate Distance Calculation
At its core, the LM algorithm operates by minimizing the sum of squared errors between predicted and observed values. In the context of coordinate distance calculation, the algorithm treats each coordinate as a data point and aims to find the most accurate distance between these points. Here’s a simplified breakdown of the process:
-
Define the Model: The LM algorithm starts by defining a mathematical model that represents the relationship between the coordinates. This model could be as simple as a straight line or as complex as a higher-order polynomial curve.
-
Initialize Parameters: The algorithm initializes the parameters of the model, which are the coefficients that determine the shape and position of the curve. These parameters are adjusted iteratively to minimize the error.
-
Calculate Residuals: For each data point (coordinate), the algorithm calculates the residual, which is the difference between the observed value (the actual coordinate) and the predicted value (the coordinate predicted by the model). Squaring these residuals ensures that positive and negative errors have the same impact on the sum.
-
Minimize Error: The LM algorithm then adjusts the model parameters to minimize the sum of squared residuals. It does this by iteratively refining the parameters, using a combination of the gradient descent method (for steepest descent) and the Gauss-Newton method (for faster convergence). This process continues until the sum of squared residuals is minimized, indicating that the model best fits the data.
-
Extract Distance: Once the model parameters are optimized, the algorithm can extract the distance between the coordinates. This distance is a direct result of the optimized model and represents the most accurate distance between the data points.
By utilizing the LM algorithm, professionals across various industries can obtain precise coordinate distances, enabling them to make informed decisions and solve complex spatial problems. Let's now explore some real-world applications and the benefits of using this algorithm.
Real-World Applications: Unleashing the Power of LM Coordinate Distance Calculations

The LM algorithm’s ability to calculate coordinate distances with precision has led to its adoption in numerous fields, each benefiting from its unique advantages.
Computer Vision and Image Processing
In computer vision, the LM algorithm is a valuable tool for tasks such as object detection and tracking. By calculating the distances between keypoints on objects, the algorithm can help identify and track objects in real-time, making it essential for applications like autonomous vehicles, robotics, and augmented reality.
For example, consider a self-driving car equipped with cameras and sensors. The LM algorithm can analyze the coordinates of detected objects, such as pedestrians or other vehicles, and calculate their distances from the car. This information is crucial for the vehicle's decision-making processes, helping it navigate safely and avoid potential collisions.
| Application | LM Algorithm Use Case |
|---|---|
| Object Detection | Identify and track objects by calculating distances between keypoints. |
| Image Registration | Align multiple images by minimizing the distance between corresponding points. |
| Facial Recognition | Match facial features by comparing the distances between key facial landmarks. |

Geospatial Analysis and Mapping
For geospatial analysts and cartographers, the LM algorithm is a game-changer. It enables accurate calculations of distances between geographical coordinates, making it possible to create precise maps, analyze spatial patterns, and optimize routes.
Imagine a logistics company planning delivery routes across a city. By inputting the coordinates of pickup and drop-off locations into the LM algorithm, the company can calculate the most efficient routes, minimizing travel time and fuel costs. This not only improves operational efficiency but also reduces the company's environmental impact.
Robotics and Autonomous Systems
In the field of robotics, the LM algorithm is instrumental in tasks like robot navigation and path planning. By calculating the distances between coordinates, robots can plan their movements and navigate complex environments with precision.
Consider a delivery robot navigating through a crowded city center. The LM algorithm can help the robot calculate the shortest path to its destination, avoiding obstacles and optimizing its route. This not only ensures timely deliveries but also enhances the robot's safety and efficiency.
Scientific Research and Data Analysis
Scientists across various disciplines, including physics, chemistry, and biology, rely on accurate coordinate distance calculations for their research. The LM algorithm provides a robust and efficient method for analyzing spatial data, leading to new insights and discoveries.
For instance, in molecular biology, the LM algorithm can be used to analyze the distances between atoms in a protein structure. This information is crucial for understanding protein folding, enzyme function, and the development of new drugs.
Benefits and Advantages of Using the LM Algorithm for Coordinate Distance Calculations
The LM algorithm offers a range of benefits that make it an attractive choice for coordinate distance calculations. Here are some key advantages:
- Accuracy: The LM algorithm provides highly accurate results, ensuring precise distance calculations. This accuracy is crucial for applications where even small errors can have significant impacts.
- Efficiency: The algorithm's iterative nature and use of gradient descent and Gauss-Newton methods make it highly efficient, allowing for rapid calculations, even for large datasets.
- Flexibility: The LM algorithm can handle a wide range of coordinate systems and data types, making it versatile and adaptable to various use cases.
- Robustness: By minimizing the sum of squared residuals, the LM algorithm is robust against outliers and noise in the data, providing reliable results even in challenging conditions.
- Easy Integration: The LM algorithm is well-established and widely supported in various programming languages and scientific computing libraries, making it easy to integrate into existing workflows.
Future Implications and Advancements
As technology continues to advance, the LM algorithm’s role in coordinate distance calculations is expected to grow even more significant. Here are some potential future developments and implications:
- Real-Time Applications: With the increasing demand for real-time data processing, the LM algorithm could be optimized for even faster calculations, enabling its use in time-critical applications like autonomous driving and robotics.
- Machine Learning Integration: The LM algorithm could be integrated with machine learning techniques to enhance its capabilities. For example, it could be used as a pre-processing step to normalize and prepare data for machine learning algorithms, improving their accuracy and performance.
- Quantum Computing: As quantum computing becomes more accessible, the LM algorithm could be adapted for quantum processors, offering even greater computational power and speed for complex coordinate distance calculations.
- Advanced Data Analysis: With the ever-growing volume of spatial data, the LM algorithm could play a crucial role in advanced data analysis techniques, such as spatial statistics and machine learning-based spatial modeling.
In conclusion, the LM algorithm's ability to calculate coordinate distances with precision and efficiency has made it an indispensable tool in various industries. From computer vision and robotics to geospatial analysis and scientific research, the LM algorithm continues to unlock new possibilities and drive innovation. By understanding and harnessing its power, professionals can streamline their workflows, make data-driven decisions, and solve complex spatial problems with confidence.
How does the LM algorithm compare to other distance calculation methods?
+The LM algorithm offers several advantages over traditional distance calculation methods. While methods like Euclidean distance or Manhattan distance are simple and fast, they assume a specific coordinate system and may not capture the true distance between coordinates. The LM algorithm, on the other hand, can handle a wide range of coordinate systems and provides more accurate results, especially for non-linear relationships between coordinates.
Can the LM algorithm handle large datasets efficiently?
+Absolutely! The LM algorithm’s iterative nature and use of efficient optimization techniques make it well-suited for large datasets. It can rapidly process and calculate distances for thousands or even millions of coordinates, making it a valuable tool for big data applications.
Are there any limitations to using the LM algorithm for coordinate distance calculations?
+While the LM algorithm is powerful, it does have some limitations. It assumes a continuous and differentiable relationship between coordinates, which may not always be the case in real-world scenarios. Additionally, the algorithm’s performance can be affected by the presence of outliers or noise in the data. However, with proper data preprocessing and error handling, these limitations can be mitigated.