Mastering the Art of 3-Variable Karnaugh Maps
Karnaugh Maps, often referred to as K-maps, are a powerful tool in digital logic design, providing an efficient method to simplify and optimize Boolean expressions. Among the various types of K-maps, the 3-variable Karnaugh Map stands out as a versatile and essential technique for digital circuit designers. This comprehensive guide aims to unravel the intricacies of 3-variable K-maps, offering a detailed insight into their creation, interpretation, and practical applications.
Understanding the Fundamentals of 3-Variable Karnaugh Maps
At the heart of digital logic design, Karnaugh Maps offer a visual representation of Boolean functions, facilitating the identification of optimal prime implicants and minimal sum-of-products expressions. This technique, first introduced by Maurice Karnaugh in 1953, has since become an indispensable tool for circuit simplification and optimization.
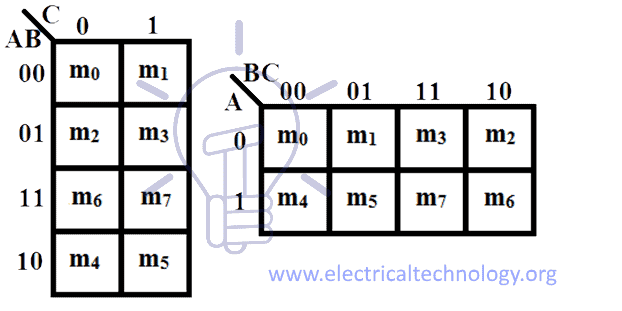
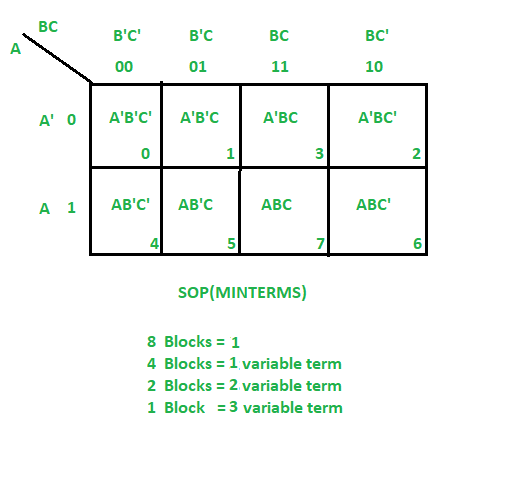
The 3-variable Karnaugh Map, specifically, is designed to handle Boolean functions with three input variables, typically denoted as A, B, and C. These maps are structured in a square format, with each cell representing a unique combination of the input variables. The rows and columns of the map are labeled with the possible values of the variables, allowing for a clear and systematic organization of the Boolean function's terms.
The process of creating a 3-variable K-map involves assigning the terms of the Boolean function to their corresponding cells, based on the input variable combinations. This step, often referred to as "mapping," sets the foundation for the subsequent simplification process. Once the terms are mapped, the map is then analyzed to identify groups of cells that form a rectangle, which represent the prime implicants of the function.
Creating and Interpreting 3-Variable Karnaugh Maps

The creation of a 3-variable Karnaugh Map begins with a thorough understanding of the Boolean function to be simplified. This function, typically represented as a sum-of-products expression, is then mapped onto the K-map, with each term occupying its respective cell. The challenge lies in arranging the terms in a way that maximizes the number of adjacent cells, as this facilitates the identification of prime implicants.
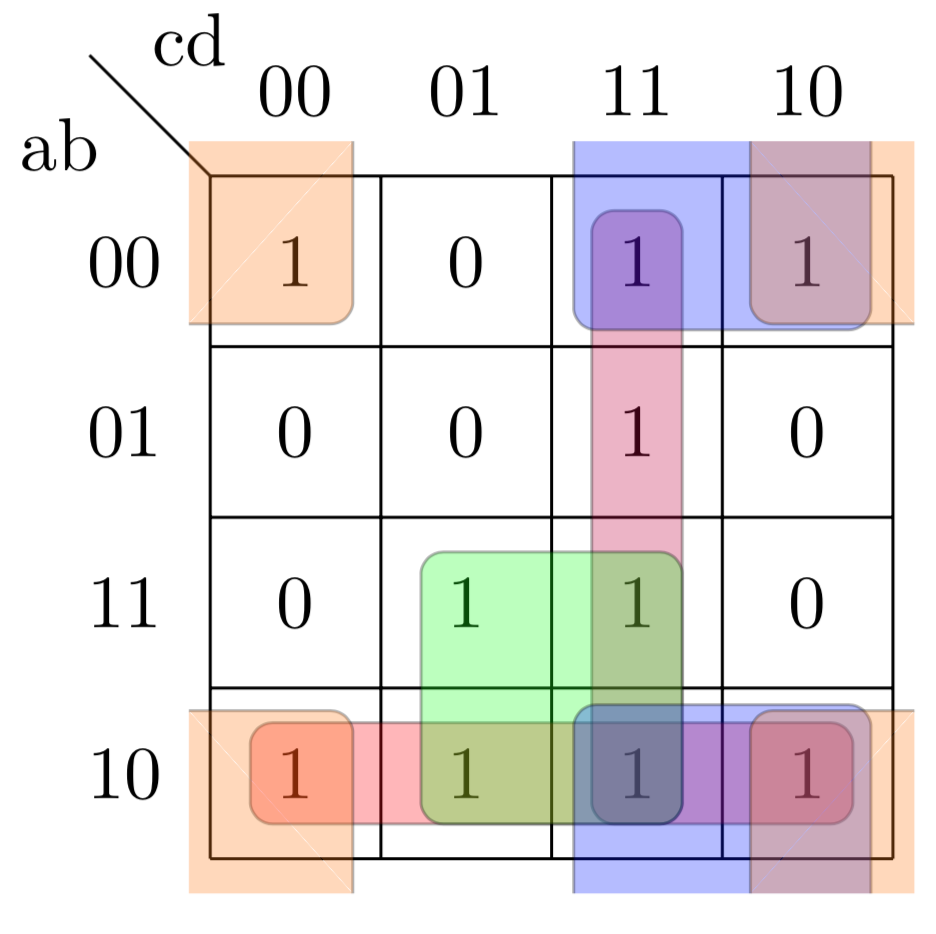
Once the mapping is complete, the interpretation phase begins. This involves identifying groups of cells that form a rectangle, with each rectangle representing a prime implicant. The cells within a rectangle should have a consistent pattern, either all 1's or all 0's. The prime implicants, along with their corresponding cover, are then used to derive the minimal sum-of-products expression for the Boolean function.
For instance, consider a Boolean function F(A, B, C) with the sum-of-products expression F = A'BC' + ABC + AB'C'. Mapping this function onto a 3-variable K-map would result in three 1's in the corresponding cells. The task then becomes to identify the prime implicants, which in this case would be A'BC' and ABC, and their covers, A'BC' and AB respectively. These prime implicants and their covers can then be used to construct the minimal sum-of-products expression for the function.
| A | B | C | F |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Advantages and Applications of 3-Variable Karnaugh Maps
The 3-variable Karnaugh Map offers several advantages over other simplification methods. Firstly, it provides a visual representation of the Boolean function, making it easier to identify patterns and optimize the function. Secondly, the map allows for a systematic approach to simplification, ensuring that all possible prime implicants are considered. This method is particularly useful for functions with a moderate number of input variables, as it strikes a balance between complexity and ease of interpretation.
The applications of 3-variable K-maps are diverse and far-reaching. They are commonly used in digital circuit design to simplify logic gates and optimize circuit performance. By reducing the number of logic gates required, K-maps can lead to more efficient and cost-effective circuit designs. Additionally, K-maps play a crucial role in the design of memory circuits, where they are used to minimize the number of memory elements required, thus enhancing the circuit's efficiency and reliability.
In the realm of digital electronics, the 3-variable Karnaugh Map is a valuable tool for students and professionals alike. It offers a straightforward and systematic approach to simplifying Boolean functions, making it an essential skill for anyone involved in digital circuit design and optimization.
Advanced Techniques and Considerations
While the basic principles of 3-variable Karnaugh Maps are straightforward, there are several advanced techniques and considerations to enhance their effectiveness. One such technique involves the use of “don’t care” conditions, which can be particularly useful when dealing with complex functions. “Don’t care” conditions refer to the cases where the value of the function does not affect the output, allowing for more flexibility in the simplification process.
Another advanced consideration is the grouping of cells on the K-map. While the primary goal is to identify prime implicants that form rectangles, there may be situations where grouping cells in a different pattern can lead to a more optimal solution. This advanced technique requires a deeper understanding of Boolean algebra and can significantly enhance the efficiency of the simplification process.
Furthermore, the application of 3-variable K-maps extends beyond digital circuit design. They are also valuable in computer science and artificial intelligence, particularly in the development of algorithms and decision-making processes. The visual representation and systematic simplification offered by K-maps make them a versatile tool in various fields, enhancing efficiency and optimizing performance.
Conclusion: Mastering the Art of 3-Variable Karnaugh Maps
Mastering the art of 3-variable Karnaugh Maps is an essential skill for anyone involved in digital logic design. By providing a visual and systematic approach to simplifying Boolean functions, K-maps offer an efficient method to optimize circuit designs and enhance performance. With a thorough understanding of the mapping process, interpretation techniques, and advanced considerations, designers can harness the full potential of 3-variable K-maps, leading to more efficient and reliable digital circuits.
As digital technology continues to evolve, the importance of tools like 3-variable Karnaugh Maps will only increase. By staying proficient in these techniques, designers can stay at the forefront of innovation, driving the development of more advanced and efficient digital systems.
What is a 3-Variable Karnaugh Map and why is it important in digital logic design?
+
A 3-Variable Karnaugh Map, or K-map, is a graphical tool used to simplify Boolean functions with three input variables. It is important in digital logic design as it provides a systematic and visual method to optimize complex Boolean expressions, leading to more efficient circuit designs.
How is a 3-variable K-map created and interpreted?
+
A 3-variable K-map is created by mapping the terms of a Boolean function onto a square grid, with each cell representing a unique combination of the input variables. Interpretation involves identifying groups of cells that form a rectangle, which represent the prime implicants of the function. These prime implicants, along with their covers, are used to derive the minimal sum-of-products expression.
What are the advantages of using 3-variable Karnaugh Maps in digital circuit design?
+
3-variable Karnaugh Maps offer a visual representation of Boolean functions, making it easier to identify patterns and optimize the function. They provide a systematic approach to simplification, ensuring that all possible prime implicants are considered. This leads to more efficient circuit designs, reduced cost, and improved performance.
Are there any advanced techniques for optimizing 3-variable Karnaugh Maps?
+
Yes, advanced techniques include the use of “don’t care” conditions, which allow for more flexibility in the simplification process. Additionally, grouping cells in a different pattern on the K-map can lead to more optimal solutions, requiring a deeper understanding of Boolean algebra.