Understanding Gradient Descent: 4 Tips
The journey into the realm of machine learning and artificial intelligence often begins with a solid grasp of optimization algorithms. Among these, Gradient Descent stands out as a fundamental concept, a cornerstone in the field of deep learning and neural networks. Its role in optimizing model parameters to minimize errors is crucial, and understanding its nuances is key to harnessing its full potential.
In this article, we will delve into the world of Gradient Descent, providing a comprehensive guide to help you grasp its intricacies and apply it effectively in your machine learning endeavors. By the end of this exploration, you should have a clear understanding of Gradient Descent's principles, its various forms, and practical tips to enhance its performance.
The Essence of Gradient Descent
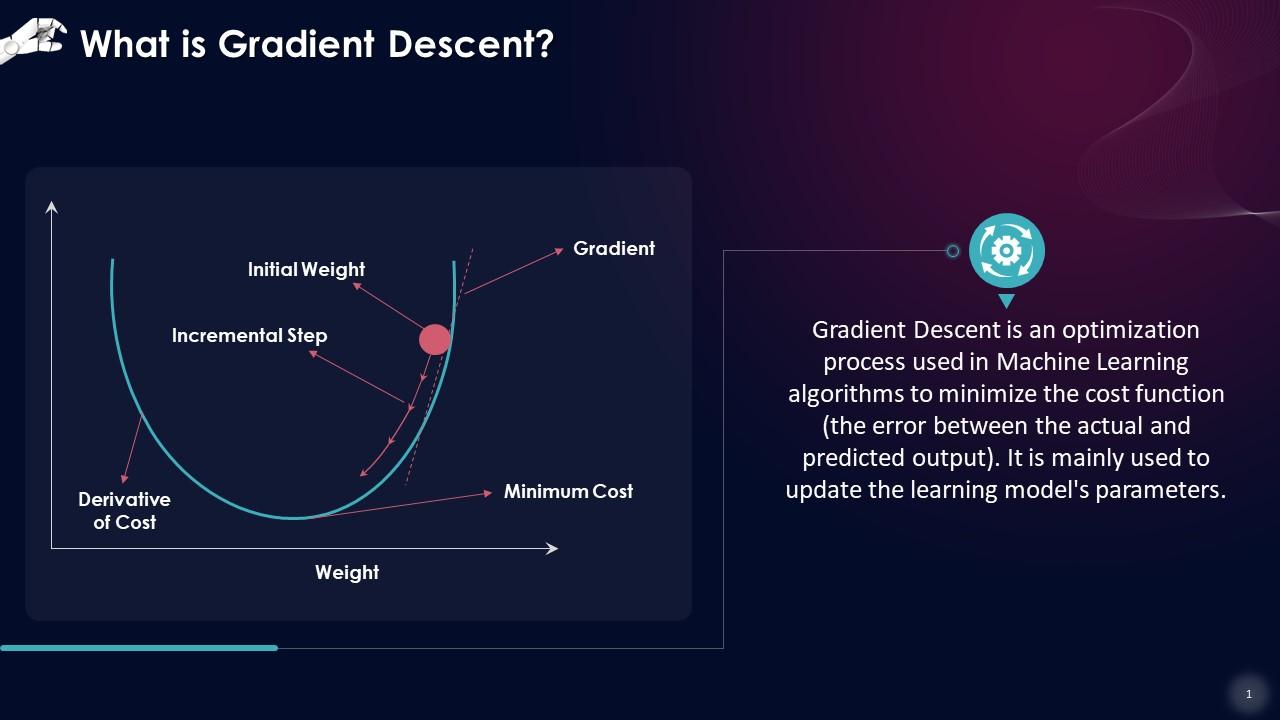
At its core, Gradient Descent is an optimization algorithm used in machine learning to iteratively adjust the parameters of a model in order to minimize a cost function. It achieves this by moving in the direction of steepest descent, taking small steps towards the minimum of the function. This process is akin to a ball rolling down a hill, where the ball’s path represents the trajectory of the parameters, and the hill’s shape corresponds to the cost function’s landscape.
Mathematically, Gradient Descent can be expressed as follows:
\[ \begin{equation*} \theta_{i+1} = \theta_{i} - \eta \cdot \nabla J(\theta_{i}) \end{equation*} \]
where $\theta$ represents the model parameters, $J(\theta)$ is the cost function, $\nabla J(\theta)$ is the gradient of the cost function with respect to $\theta$, and $\eta$ is the learning rate, a hyperparameter that controls the step size in the descent.
The algorithm works by repeatedly updating the model parameters $\theta$ in the opposite direction of the gradient, moving towards the function's minimum. This iterative process continues until the algorithm converges, indicating that the model has found the optimal parameters that minimize the cost function.
The Importance of Gradient Descent in Machine Learning
Gradient Descent is a ubiquitous algorithm in machine learning, serving as the backbone for training various models, particularly in the context of deep learning. Its ability to optimize model parameters makes it a crucial tool for tasks such as image classification, natural language processing, and predictive analytics.
By effectively minimizing the cost function, Gradient Descent ensures that the model learns from data, improving its performance over time. This iterative optimization process is at the heart of many successful machine learning applications, driving the development of intelligent systems that can tackle complex problems.
Exploring the Variants of Gradient Descent

While the basic concept of Gradient Descent remains consistent, several variants have emerged to address specific challenges and optimize performance in different scenarios. Here, we delve into some of the most prominent forms of Gradient Descent.
Batch Gradient Descent
Batch Gradient Descent is the simplest form of Gradient Descent, where the gradient is calculated using the entire training dataset. This approach provides an accurate estimate of the gradient but can be computationally expensive, especially for large datasets. The update equation for Batch Gradient Descent is:
\[ \begin{equation*} \theta_{i+1} = \theta_{i} - \eta \cdot \frac{1}{m} \sum_{j=1}^{m} \nabla J(\theta; x^{(j)}, y^{(j)}) \end{equation*} \]
where $m$ is the number of training examples, $x^{(j)}$ and $y^{(j)}$ are the $j$-th training example and its corresponding label, respectively.
Stochastic Gradient Descent (SGD)
Stochastic Gradient Descent is a variant that calculates the gradient using a single training example at each iteration. This approach is computationally efficient and allows for faster convergence, especially in large-scale datasets. However, SGD can be less accurate due to the noisy gradient estimates. The update equation for SGD is:
\[ \begin{equation*} \theta_{i+1} = \theta_{i} - \eta \cdot \nabla J(\theta; x^{(i)}, y^{(i)}) \end{equation*} \]
where $x^{(i)}$ and $y^{(i)}$ are the $i$-th training example and its corresponding label.
Mini-Batch Gradient Descent
Mini-Batch Gradient Descent strikes a balance between Batch Gradient Descent and SGD by calculating the gradient using a small batch of training examples at each iteration. This approach combines the efficiency of SGD with the accuracy of Batch Gradient Descent, making it a popular choice in practice. The update equation for Mini-Batch Gradient Descent is:
\[ \begin{equation*} \theta_{i+1} = \theta_{i} - \eta \cdot \frac{1}{b} \sum_{j=1}^{b} \nabla J(\theta; x^{(i,j)}, y^{(i,j)}) \end{equation*} \]
where $b$ is the batch size, and $x^{(i,j)}$ and $y^{(i,j)}$ are the $j$-th training example and its corresponding label in the $i$-th batch.
Adaptive Gradient Descent Algorithms
Adaptive Gradient Descent algorithms adjust the learning rate dynamically during training. These algorithms aim to address the issue of choosing an appropriate learning rate, as a fixed learning rate may not be optimal for all parameters. Some popular adaptive algorithms include AdaGrad, RMSProp, and Adam.
| Algorithm | Learning Rate Adaptation |
|---|---|
| AdaGrad | Adjusts the learning rate for each parameter based on the square root of the sum of all past squared gradients. |
| RMSProp | Similar to AdaGrad, but uses a moving average of the squared gradients, providing a smoother learning rate adjustment. |
| Adam | Combines the ideas of AdaGrad and RMSProp, using both the mean and variance of the gradients to adjust the learning rate. |
Tips for Enhancing Gradient Descent Performance
To ensure the effectiveness and efficiency of Gradient Descent, it’s crucial to consider various factors that can influence its performance. Here are some practical tips to optimize the Gradient Descent algorithm in your machine learning models.
1. Choosing the Right Learning Rate
The learning rate, denoted by \eta, is a critical hyperparameter that controls the step size in the descent. A learning rate that is too small can lead to slow convergence, while a learning rate that is too large may cause the algorithm to overshoot the minimum or even diverge. It’s essential to choose an appropriate learning rate for your specific problem.
There are several strategies to determine the optimal learning rate, including:
- Grid Search: Try out different learning rates and evaluate the model's performance. This can be computationally expensive but provides an accurate estimate.
- Learning Rate Scheduling: Adjust the learning rate dynamically during training. This can be done by reducing the learning rate after a certain number of iterations or when the model's performance plateaus.
- Adaptive Learning Rates: Use adaptive algorithms like AdaGrad, RMSProp, or Adam, which adjust the learning rate based on the gradients' history.
2. Batch Size Selection
In Mini-Batch Gradient Descent, the choice of batch size, denoted by b, can significantly impact the algorithm’s performance. A larger batch size provides a more accurate gradient estimate but can be computationally expensive. Conversely, a smaller batch size may result in noisy gradient estimates but allows for faster iterations.
Experimenting with different batch sizes and evaluating the model's performance can help determine the optimal batch size for your specific problem.
3. Regularization Techniques
Regularization techniques are essential to prevent overfitting and improve the generalization ability of your model. Two common regularization methods include L1 Regularization and L2 Regularization, also known as Lasso and Ridge regression, respectively.
L1 Regularization adds the absolute value of the model's parameters to the cost function, encouraging sparse models. L2 Regularization adds the square of the model's parameters to the cost function, penalizing large parameter values.
The choice of regularization technique depends on the specific problem and the model's architecture. It's essential to experiment with different regularization methods and evaluate their impact on the model's performance.
4. Early Stopping
Early stopping is a technique used to prevent overfitting by stopping the training process before the model begins to memorize the training data. This is achieved by monitoring the model’s performance on a validation set and stopping the training when the performance on the validation set starts to degrade.
By implementing early stopping, you can ensure that your model generalizes well to unseen data, preventing it from overfitting to the training examples.
Conclusion
Gradient Descent is a powerful optimization algorithm that forms the foundation of many machine learning models, particularly in the context of deep learning. Understanding its variants and optimizing its performance through careful hyperparameter tuning, regularization, and early stopping can significantly enhance the accuracy and efficiency of your models.
By exploring the concepts presented in this article, you should now have a deeper understanding of Gradient Descent and be equipped with practical tips to improve its performance in your machine learning endeavors. With this knowledge, you're ready to tackle more complex optimization challenges and continue your journey in the fascinating world of artificial intelligence and machine learning.
How does Gradient Descent work in practice?
+In practice, Gradient Descent is implemented as an iterative algorithm. It starts with an initial guess for the model parameters, then calculates the gradient of the cost function with respect to these parameters. Using this gradient, the algorithm updates the parameters in the opposite direction of the gradient, moving towards the minimum of the cost function. This process is repeated until the algorithm converges or reaches a specified number of iterations.
What are the challenges in implementing Gradient Descent?
+Implementing Gradient Descent effectively requires careful consideration of several factors. One of the main challenges is choosing an appropriate learning rate. A learning rate that is too large may cause the algorithm to diverge, while a learning rate that is too small can lead to slow convergence. Additionally, the choice of batch size in Mini-Batch Gradient Descent can impact the algorithm’s performance and convergence rate.
Can Gradient Descent guarantee convergence to the global minimum?
+In theory, Gradient Descent can guarantee convergence to a global minimum under certain conditions. These conditions include a continuously differentiable and convex cost function. However, in practice, the cost function may have multiple local minima or saddle points, making it challenging to guarantee convergence to the global minimum. In such cases, techniques like random restarts or adaptive learning rates can be used to improve the chances of finding the global minimum.
What are some common pitfalls to avoid when using Gradient Descent?
+When working with Gradient Descent, there are a few common pitfalls to be aware of. One is the choice of an inappropriate learning rate, which can lead to slow convergence or divergence. Another pitfall is overfitting, where the model becomes too complex and starts to memorize the training data instead of generalizing to new examples. Regularization techniques and early stopping can help mitigate overfitting.