5 Ways to Master Z Scores in R

Z-scores, also known as standard scores, are a powerful statistical tool used to standardize data and compare values across different distributions. In the realm of data analysis, particularly when working with the R programming language, understanding and mastering Z-scores is essential for gaining deeper insights into your data. This article will guide you through five effective strategies to become a pro at working with Z-scores in R, enabling you to perform more sophisticated data analyses and draw meaningful conclusions.

1. Understanding the Concept of Z-Scores

Z-scores are a measure of how many standard deviations a data point is from the mean of a dataset. In other words, they represent the normalized value of a data point relative to the dataset’s average. By converting raw data values into Z-scores, we can compare data points from different datasets or variables on a common scale. This standardization process is crucial when we want to analyze and interpret data consistently, regardless of the scale or variability of the original data.

The formula for calculating Z-scores is straightforward: Z = (X - μ) / σ, where X is the raw data value, μ is the mean of the dataset, and σ is the standard deviation. This formula essentially transforms the data into a standard normal distribution, where the mean is 0 and the standard deviation is 1.

For example, let's consider a dataset of student test scores. We want to analyze the performance of these students relative to the average score. By calculating Z-scores for each student's score, we can identify those who performed exceptionally well or fell behind, regardless of the overall variability in the scores.

Benefits of Using Z-Scores

The primary advantage of Z-scores is their ability to simplify data interpretation. By standardizing data, we can easily identify outliers, assess the distribution of values, and make meaningful comparisons between datasets. Z-scores also enable us to apply various statistical techniques, such as hypothesis testing and regression analysis, to our data with greater accuracy and interpretability.

2. Generating Z-Scores in R

R provides a range of functions and packages that make generating Z-scores a breeze. One of the most commonly used functions is scale(), which standardizes the columns of a data frame or matrix by removing the mean and scaling to unit variance.

For instance, to generate Z-scores for a dataset named student_scores, we can use the following code:

z_scores <- scale(student_scores)

# To retrieve the standardized values
z_scores$scale

The scale() function returns a list with two components: scale and center. The scale component contains the standardized values (Z-scores), while the center component holds the mean values used for standardization.

Additionally, the dplyr package offers the mutate_at() function, which allows us to apply transformations to specific columns of a data frame. We can utilize this function to calculate Z-scores for selected variables.

library(dplyr)

# Calculating Z-scores for 'Math' and 'Science' scores
student_scores <- student_scores %>%
  mutate_at(vars(Math, Science), scale)

In this example, we used mutate_at() to create new columns with the Z-scores for the 'Math' and 'Science' variables.

Advanced Z-Score Generation

For more advanced Z-score calculations, the stats package provides the scaleNorm() function, which allows us to specify the mean and standard deviation values for standardization.

library(stats)

# Calculating Z-scores with custom mean and standard deviation
z_scores <- scaleNorm(student_scores, mean = 75, sd = 15)

By using scaleNorm(), we have greater control over the standardization process, enabling us to apply specific scaling factors to our data.

3. Interpreting and Visualizing Z-Scores

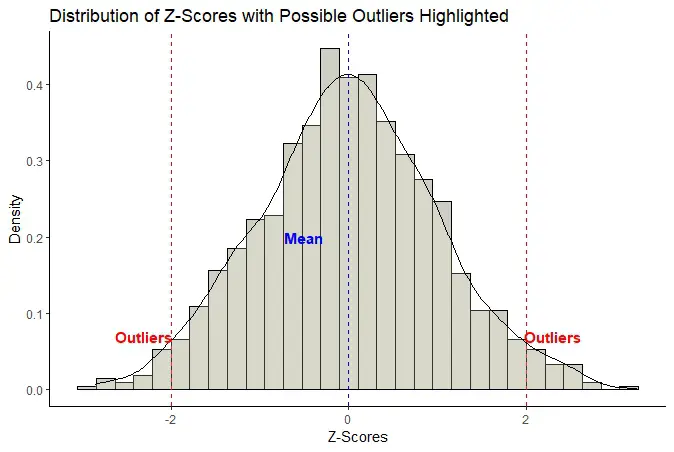
Once we have generated Z-scores, interpreting and visualizing them becomes crucial for gaining insights into our data. Z-scores follow a standard normal distribution, which means that approximately 68% of the data points fall within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations.

By plotting Z-scores on a histogram or density plot, we can visually assess the distribution of our data. For example, a bell-shaped curve centered around zero indicates a normal distribution, while a skewed distribution may suggest the presence of outliers or data points that deviate significantly from the mean.

hist(z_scores, main = "Histogram of Z-Scores", xlab = "Z-Scores")

The hist() function generates a histogram of the Z-scores, allowing us to visually inspect the distribution. We can also use the ggplot2 package to create more customizable and visually appealing plots.

library(ggplot2)

ggplot(data.frame(z_scores), aes(x = z_scores)) +
  geom_histogram(binwidth = 0.5) +
  labs(title = "Histogram of Z-Scores", x = "Z-Scores")

This code creates a histogram using ggplot2, with customizable bin width and labels.

Outlier Detection with Z-Scores

Z-scores are particularly useful for identifying outliers in our data. Data points with Z-scores greater than 3 or less than -3 are typically considered outliers, as they fall outside the range of typical data values. By setting appropriate thresholds for Z-scores, we can flag these outliers and investigate them further.

outliers <- z_scores[z_scores < -3 | z_scores > 3]

# To view the outliers
outliers

The above code snippet identifies and extracts outliers from the Z-scores dataset.

4. Applying Z-Scores in Statistical Analyses

Z-scores are not just a tool for data visualization and interpretation; they are also integral to various statistical analyses. By standardizing our data, we can perform more advanced analyses with greater accuracy and interpretability.

Hypothesis Testing with Z-Scores

In hypothesis testing, Z-scores are used to calculate test statistics, such as the Z-statistic, which measures the strength of evidence against the null hypothesis. By converting our data into Z-scores, we can perform one-sample or two-sample Z-tests to determine whether the mean of a population is significantly different from a hypothesized value or whether the means of two populations are significantly different.

The stats package provides the pnorm() function to calculate the probability associated with a given Z-score. This function is crucial for determining the p-value in hypothesis testing.

library(stats)

# Calculating the p-value for a Z-score
pnorm(z_score, lower.tail = FALSE)

The pnorm() function calculates the probability of obtaining a Z-score greater than or equal to the given value. By setting lower.tail = FALSE, we specify that we are interested in the upper tail probability, which is often used in hypothesis testing.

Regression Analysis with Z-Scores

Z-scores are valuable in regression analysis, especially when dealing with datasets that have variables on different scales. By standardizing the predictors (independent variables) to have a mean of zero and a standard deviation of one, we can ensure that the coefficients in the regression model are on a comparable scale. This standardization process helps in interpreting the relative importance of each predictor and in assessing the overall fit of the model.

model <- lm(y ~ scale(x1) + scale(x2) + ..., data = dataset)

In this example, we use the lm() function to fit a linear regression model, where x1 and x2 are standardized using the scale() function. This ensures that the coefficients are interpreted in relation to a standard deviation change in the predictor variables.

5. Advanced Techniques for Z-Score Analysis

While the basic techniques for generating and interpreting Z-scores are powerful, there are advanced methods that can further enhance our analysis. These techniques involve more complex statistical concepts and are particularly useful when dealing with large datasets or specific research questions.

Z-Score Transformation for Non-Normal Data

In some cases, our data may not follow a normal distribution, which is a common assumption for many statistical tests and analyses. When this happens, we can apply a Z-score transformation to normalize the data and make it more suitable for analysis. The Box-Cox transformation is a popular method for achieving this.

The Box-Cox transformation is defined as Y'(λ) = (Y^λ - 1) / λ, where Y is the original data value, λ is a parameter to be estimated, and Y' is the transformed value. This transformation helps to normalize the data and make it more amenable to standard statistical techniques.

The MASS package in R provides the boxcox() function to estimate the optimal λ value for the transformation. Once we have the λ value, we can apply the transformation to our data.

library(MASS)

# Estimating the optimal lambda value
boxcox_results <- boxcox(y ~ 1, data = dataset)
lambda <- boxcox_results$lambda

# Applying the Box-Cox transformation
transformed_data <- (dataset$y^lambda - 1) / lambda

Z-Score-Based Clustering and Dimension Reduction

Z-scores can also be used in clustering algorithms and dimension reduction techniques to identify patterns and structures in our data. By converting our data into Z-scores, we can apply algorithms such as K-means clustering or Principal Component Analysis (PCA) to group similar data points and reduce the dimensionality of our dataset.

For example, the factoextra package provides functions for clustering and visualizing clusters based on Z-scores. The fviz_cluster() function can be used to create beautiful cluster plots, while the fviz_pca_ind() function helps in visualizing the contribution of each variable to the principal components.

library(factoextra)

# K-means clustering based on Z-scores
km_results <- kmeans(scale(dataset), centers = 3)

# Visualizing the clusters
fviz_cluster(km_results, data = dataset, ellipse = TRUE)

This code snippet demonstrates how to perform K-means clustering on Z-score-transformed data and visualize the clusters using fviz_cluster().

Conclusion

Mastering Z-scores in R is a crucial skill for data analysts and researchers. By understanding the concept of Z-scores and learning how to generate, interpret, and apply them in various statistical analyses, we can unlock the full potential of our data. Z-scores provide a standardized and comparable scale for data analysis, enabling us to make more informed decisions and draw meaningful conclusions from our datasets.

Throughout this article, we explored the fundamental concepts of Z-scores, delved into practical techniques for generating and visualizing them, and discussed their applications in hypothesis testing and regression analysis. We also covered advanced topics such as Z-score transformation for non-normal data and its use in clustering and dimension reduction. By implementing these strategies, you'll be well-equipped to tackle complex data analysis tasks and contribute valuable insights to your field of study.

Frequently Asked Questions