The Fraction for 0.45: Simple Math.

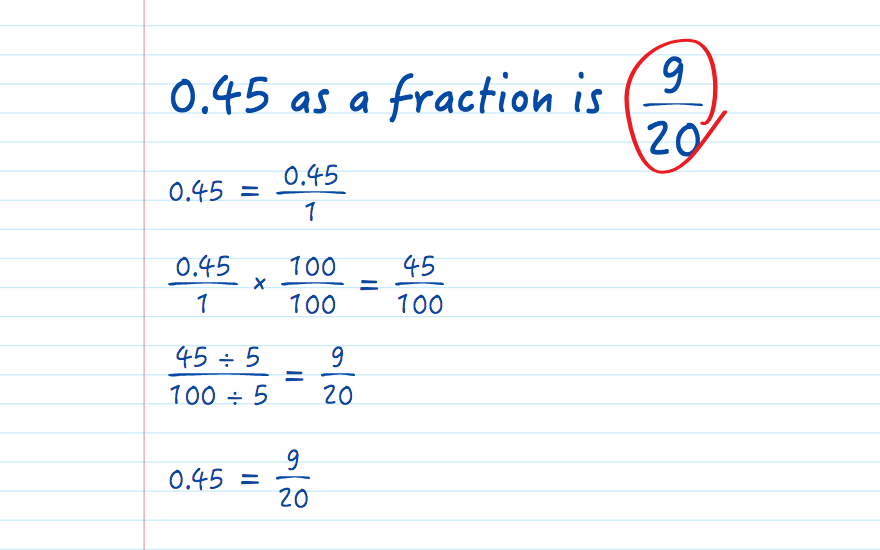
Math enthusiasts and scholars often encounter a wide array of numerical representations, and understanding their conversions is essential for comprehensive mathematical knowledge. One such representation is the fraction equivalent of the decimal number 0.45. This seemingly simple conversion holds importance in various mathematical applications, from basic arithmetic to advanced calculations. Let's delve into the world of fractions and explore the significance of this conversion.

The Conversion: 0.45 to Fraction

Converting a decimal number to its fraction form involves understanding the relationship between the decimal and its place value. In the case of 0.45, the decimal is composed of two parts: the whole number 0 and the fractional part 45 (which represents ⁴⁵⁄₁₀₀ when considering the place value of tenths and hundredths). To simplify this fraction, we divide both the numerator and denominator by their greatest common divisor, which is 5 in this case. Thus, the simplified fraction equivalent of 0.45 is ⁹⁄₂₀.

The Significance of Fraction Representation

Fractions are more than just numerical representations; they carry practical significance in various mathematical contexts. Here’s why understanding fraction conversions is essential:

Precision and Accuracy

Fractions provide a more precise representation of quantities, especially when dealing with measurements or calculations that require high accuracy. For instance, in engineering or scientific applications, using fractions can ensure that critical values are not rounded off, leading to more precise outcomes.

Algebraic Manipulations

In algebraic expressions and equations, fractions play a pivotal role. They allow for the manipulation and simplification of equations, making it easier to solve complex problems. Understanding fraction conversions ensures that algebraic operations are performed accurately and efficiently.

Real-World Applications

Fractions are an integral part of our daily lives. From cooking recipes (where ingredient quantities are often represented as fractions) to construction projects (involving measurements in fractions of feet or inches), a solid understanding of fraction conversions is invaluable.

Applications in Advanced Mathematics

While the conversion of 0.45 to ⁹⁄₂₀ may seem basic, it forms the foundation for more complex mathematical concepts. Here’s how this conversion extends into advanced mathematics:

Limits and Continuity

In calculus, understanding fraction conversions is crucial when dealing with limits and continuity. For instance, when finding the limit of a function as it approaches a certain value, the ability to convert between decimals and fractions ensures accurate evaluations.

Complex Numbers

Complex numbers, often represented in rectangular form as a + bi, where a and b are real numbers, and i is the imaginary unit, can be manipulated using fraction conversions. This is especially important in electrical engineering and signal processing, where complex numbers are widely used.

Advanced Statistics

In advanced statistical analyses, especially when dealing with probability distributions or Bayesian statistics, fractions are commonly used to represent probabilities. Understanding fraction conversions ensures that statistical calculations are accurate and reliable.

Educational Importance

Teaching students the conversion between decimals and fractions is an essential part of mathematics education. It not only enhances their understanding of numerical representations but also prepares them for more advanced mathematical concepts. Here’s why this conversion is emphasized in educational curricula:

Building Mathematical Foundation

Converting between decimals and fractions helps students grasp the fundamental concept of place value and how it affects numerical representations. This foundational understanding is crucial for building more complex mathematical skills.

Problem-Solving Skills

By practicing fraction conversions, students develop problem-solving skills. They learn to approach mathematical problems from different angles, enhancing their critical thinking abilities.

Real-Life Connections

Introducing fraction conversions in the early stages of mathematics education helps students connect mathematical concepts with real-life situations. This connection makes learning more engaging and meaningful.

Conclusion

The conversion of 0.45 to its fraction form, ⁹⁄₂₀, is more than just a simple mathematical operation. It represents a fundamental understanding of numerical representations and their applications in various mathematical contexts. From precision in measurements to advanced algebraic manipulations, fractions are an integral part of the mathematical landscape. As such, a solid grasp of fraction conversions is essential for both mathematical proficiency and real-world problem-solving.