Two-Way ANOVA: 8 Key Insights
The Two-Way Analysis of Variance (ANOVA) is a powerful statistical technique that allows researchers and analysts to delve into the intricate relationships between variables. This method, with its ability to assess the impact of multiple factors on a response variable, has found extensive application across various fields, including psychology, biology, and economics. In this comprehensive guide, we will explore the nuances of Two-Way ANOVA, providing insights into its utility, methodology, and real-world implications.
Understanding Two-Way ANOVA
Two-Way ANOVA is a statistical tool designed to analyze the impact of two independent variables (also known as factors) on a single dependent variable. This technique is particularly valuable when researchers aim to understand the joint and individual effects of these factors on the response variable. By examining the interaction between the two factors, Two-Way ANOVA helps in identifying whether the impact of one factor depends on the levels of the other factor.
Key Insights and Applications
Let’s delve into the eight key insights that make Two-Way ANOVA an indispensable tool for researchers and analysts.
1. Exploring Factor Interactions
One of the primary strengths of Two-Way ANOVA lies in its ability to assess factor interactions. Researchers can determine whether the effect of one factor on the dependent variable is influenced by the levels of the other factor. This insight is crucial in understanding complex relationships and can lead to more accurate interpretations of data.
| Factor A | Factor B | Dependent Variable |
|---|---|---|
| High | Low | 12 |
| High | Medium | 18 |
| High | High | 20 |
| Low | Low | 8 |
| Low | Medium | 10 |
| Low | High | 14 |

2. Individual Factor Effects
Two-Way ANOVA also provides insights into the individual effects of each factor. Researchers can determine whether a single factor has a significant impact on the dependent variable, even when controlling for the other factor. This analysis is crucial for understanding the unique contributions of each factor to the observed outcomes.
3. Statistical Power and Sample Size
When designing experiments, researchers must consider the statistical power of their study. Two-Way ANOVA can help determine the sample size required to detect significant effects. By understanding the power of their study, researchers can ensure they collect enough data to make accurate conclusions.
4. Multiple Comparisons and Adjustments
In Two-Way ANOVA, when significant interactions are detected, it becomes necessary to perform multiple comparisons to understand the specific differences between factor levels. Various methods, such as the Tukey’s HSD test, can be employed to adjust for these comparisons, ensuring accurate and reliable results.
5. Assumptions and Violations
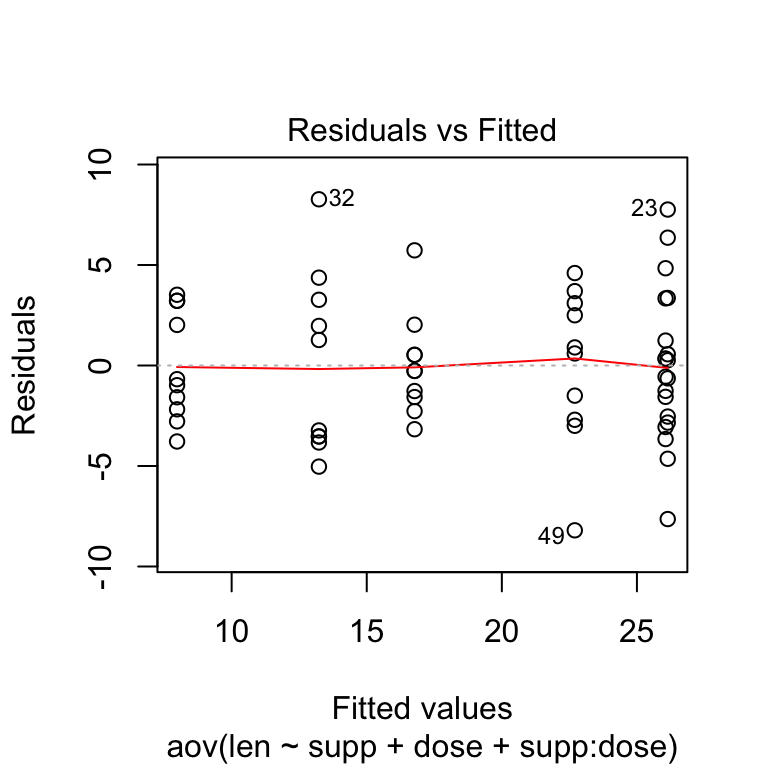
Like any statistical method, Two-Way ANOVA relies on certain assumptions. Researchers must be aware of these assumptions and potential violations. Common assumptions include independence of observations, normality of residuals, and homogeneity of variances. Understanding these assumptions and their violations is crucial for interpreting the results accurately.
6. Model Selection and Design
Choosing the appropriate model for Two-Way ANOVA is a critical step. Researchers must consider the research question, the nature of the factors, and the expected interactions. The design of the experiment, including the number of levels for each factor and the sample size, should be carefully planned to align with the research objectives.
7. Post-Hoc Analysis
In cases where the ANOVA results indicate significant effects or interactions, post-hoc analysis becomes essential. This analysis involves examining specific contrasts or comparisons between factor levels to understand the nature of the significant findings. Techniques like the Bonferroni correction can be used to control for multiple comparisons and ensure reliable conclusions.
8. Interpreting Effect Sizes
Beyond statistical significance, understanding the effect sizes is crucial for interpreting the practical significance of the findings. Measures like eta-squared or omega-squared provide insights into the proportion of variance in the dependent variable explained by the factors. This information helps researchers assess the practical importance of their results.
Real-World Applications
Two-Way ANOVA finds extensive application across various fields. For instance, in psychological research, it can be used to examine the impact of different teaching methods (Factor A) and student engagement levels (Factor B) on academic performance. In biology, researchers might explore the effects of different drug dosages (Factor A) and treatment durations (Factor B) on disease remission rates.
The versatility of Two-Way ANOVA makes it a valuable tool for researchers aiming to uncover complex relationships and make informed decisions based on statistical evidence.
What is the difference between One-Way and Two-Way ANOVA?
+
One-Way ANOVA analyzes the impact of a single factor on a dependent variable, while Two-Way ANOVA examines the effects of two independent variables on a response variable. Two-Way ANOVA provides insights into factor interactions and individual effects, making it more complex but offering a more comprehensive understanding of the data.
How is Two-Way ANOVA different from multiple regression analysis?
+
Two-Way ANOVA and multiple regression analysis are both techniques for analyzing the relationship between variables. However, Two-Way ANOVA is specifically designed for categorical independent variables and focuses on interactions. Multiple regression analysis, on the other hand, is more flexible and can handle continuous independent variables, but it may not provide the same level of detail regarding interactions.
What are some common assumptions for Two-Way ANOVA, and how can they be checked?
+
Common assumptions for Two-Way ANOVA include independence of observations, normality of residuals, and homogeneity of variances. These assumptions can be checked using graphical methods, such as residual plots and normality tests, and by examining the homogeneity of variance assumption using tests like Levene’s test or Bartlett’s test.



