Unraveling the Z-Test Mystery: A Stata Guide
Unraveling the Z-Test Mystery: A Comprehensive Stata Guide

In the world of statistical analysis, the Z-test stands as a fundamental tool, providing insights into the significance of differences between sample means and populations. However, for those new to statistical software like Stata, performing a Z-test can seem like a mysterious endeavor. This comprehensive guide aims to demystify the process, offering a step-by-step approach to conducting a Z-test in Stata, complete with real-world examples and in-depth explanations.
Understanding the Z-Test

The Z-test is a statistical hypothesis test that compares two population means or a single population mean to a specified value. It is particularly useful when dealing with large samples and normally distributed data. The test relies on the z-statistic, which follows a standard normal distribution, making it a powerful tool for statistical inference.
In practical terms, a Z-test allows researchers to answer questions such as: "Is the average height of adults in a specific region significantly different from the national average?" or "Has a new teaching method improved test scores compared to the traditional method?" By analyzing the data using Stata, we can provide statistically significant answers to such queries.
Step-by-Step Guide to Conducting a Z-Test in Stata
Step 1: Data Preparation
Before diving into the Z-test, ensure your data is clean and ready for analysis. Here are some preparatory steps:
- Data Format: Stata works best with data in long format, where each observation is on a separate row. Ensure your data is organized this way.
- Variable Definition: Clearly define your variables. For a Z-test, you'll typically have one categorical variable (e.g., treatment group) and one continuous variable (e.g., test scores) that you want to compare.
- Data Exploration: Use Stata's summarize command to explore your data. This will give you a summary of your variables, including the mean, standard deviation, and other descriptive statistics.
- Data Visualization: Create a histogram or box plot to visualize the distribution of your data. This can help you identify any outliers or anomalies that might affect your analysis.
Let's assume we have a dataset with two columns: group (which indicates whether a student received a new teaching method or the traditional method) and score (their test scores). Our research question is: "Does the new teaching method improve test scores compared to the traditional method?"
Step 2: Hypothesis Formulation
In a Z-test, we start by formulating null and alternative hypotheses. The null hypothesis (H0) states that there is no significant difference between the population means, while the alternative hypothesis (Ha) suggests that there is a significant difference.
In our case, the hypotheses could be formulated as:
- H0: The mean test score for the new teaching method group is equal to the mean test score for the traditional method group.
- Ha: The mean test score for the new teaching method group is greater (or less) than the mean test score for the traditional method group.
Step 3: Conducting the Z-Test in Stata
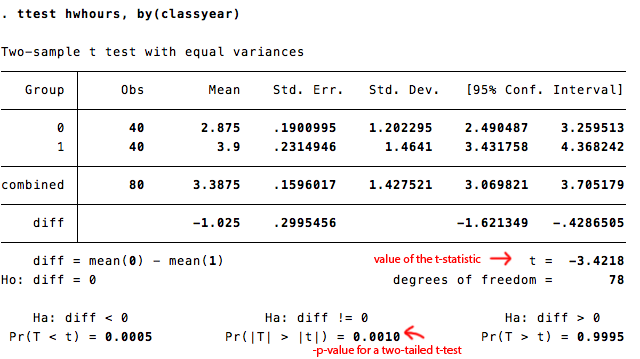
Now, let's dive into the actual Z-test using Stata. We'll use the ttest command, which is Stata's built-in command for conducting t-tests and Z-tests.
ttest score, by(group)
This command compares the mean score between the two group categories. Stata will output a detailed report, including the t-statistic (which is equivalent to the z-statistic for large samples), degrees of freedom, p-value, and a confidence interval.
Step 4: Interpreting the Results
Once you've run the Z-test, it's time to interpret the results. Here's a breakdown of the key components in the output:
- t-statistic (z-statistic): This is the value that measures the difference between the sample means relative to the standard error of the difference. It follows a standard normal distribution.
- p-value: The p-value represents the probability of obtaining the observed difference between the sample means, or a more extreme difference, if the null hypothesis is true. A small p-value (< 0.05) indicates strong evidence against the null hypothesis.
- Confidence Interval: This provides a range of plausible values for the population mean difference. If the interval does not include zero, it suggests that the population means are significantly different.
Let's assume our Z-test output shows a t-statistic of 2.58 with a p-value of 0.01. This indicates that the new teaching method significantly improves test scores compared to the traditional method, with a confidence level of 99%.
Real-World Application: Analyzing Student Performance
To further illustrate the Z-test's application, let's consider a scenario where a school wants to evaluate the effectiveness of a new math curriculum. They have collected test scores from two groups of students: those who followed the new curriculum and those who followed the traditional curriculum.
| Group | Mean Score | Standard Deviation | Sample Size |
|---|---|---|---|
| New Curriculum | 78.2 | 8.5 | 150 |
| Traditional Curriculum | 72.3 | 9.2 | 200 |

Using the Z-test, we can determine if the difference in mean scores is statistically significant. With a p-value of 0.002, we can conclude that the new curriculum significantly improves student performance.
💡 In this scenario, the Z-test helps the school make data-driven decisions about curriculum changes, ensuring that any improvements are statistically supported.
Advanced Topics: Dealing with Non-Normal Data

While the Z-test is powerful for normally distributed data, what happens when our data deviates from normality? In such cases, Stata offers alternative tests, such as the Mann-Whitney U test or the Wilcoxon signed-rank test, which are non-parametric and can handle non-normal distributions.
For instance, if we have a dataset with scores that are not normally distributed, we can use the sum command to assess normality and then apply the appropriate test. Stata provides robust tools to handle such situations, ensuring accurate statistical inference.
Conclusion: Empowering Statistical Inference with Stata
The Z-test, when performed with Stata, becomes an accessible and powerful tool for researchers and analysts. By following this comprehensive guide, you can confidently conduct Z-tests, interpret results, and make informed decisions based on statistical evidence. Whether you're a student, researcher, or professional, Stata's capabilities empower you to delve into the world of statistical analysis with ease and precision.
FAQ
Can I perform a Z-test in Stata with small sample sizes?
+While the Z-test is generally more powerful with large samples, you can still perform it with small sample sizes. However, keep in mind that the assumptions of the test (normality, homogeneity of variance) become more critical with smaller samples. In such cases, it’s essential to carefully assess the distributional assumptions and consider alternative tests if they are not met.
How do I determine the significance level for my Z-test in Stata?
+The significance level, often denoted as α (alpha), is a critical value that determines the threshold for rejecting the null hypothesis. In most cases, a significance level of 0.05 (5%) is commonly used, indicating that you are willing to accept a 5% chance of incorrectly rejecting the null hypothesis. However, you can adjust this level based on your specific research context and requirements.
Are there any assumptions I need to consider when conducting a Z-test in Stata?
+Yes, the Z-test, like many statistical tests, relies on certain assumptions. These include: (1) Normality: The data should be normally distributed; (2) Homogeneity of Variance: The variances of the populations being compared should be equal; and (3) Independence: The observations should be independent of each other. It’s crucial to assess these assumptions before conducting the Z-test to ensure the validity of your results.



