The Mod Function's Secrets: 3 Tips
Welcome, fellow mathematicians and programming enthusiasts! Today, we delve into the intriguing world of the modulo function, a mathematical concept with surprising depths. This operation, often denoted as mod, is a fundamental tool in number theory and computer science, yet it holds secrets that many may overlook. Let's uncover these hidden gems and explore three practical tips that will enhance your understanding and application of the modulo function.
1. Unraveling the Modulo Mystery: A Journey Beyond Remainders

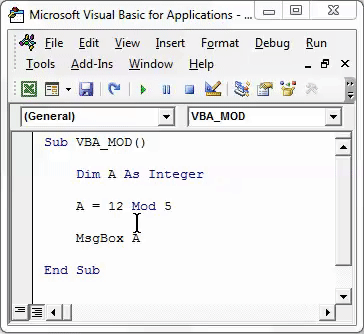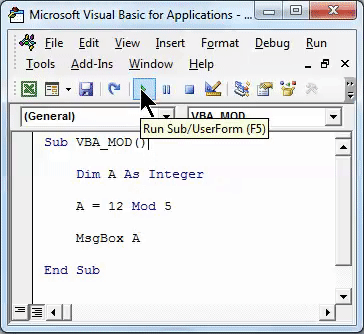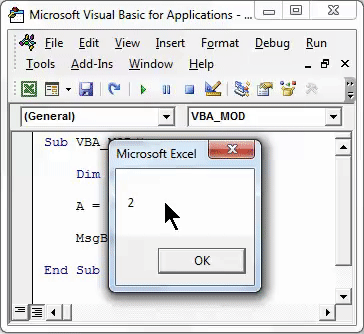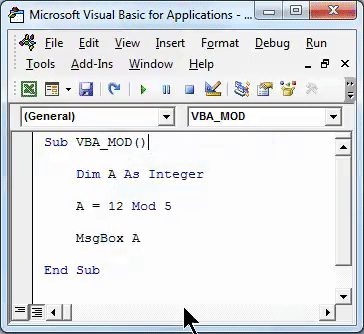
When we first encounter the modulo function, it is typically introduced as a way to find the remainder when one number is divided by another. For instance, 7 mod 3 equals 1, indicating that 7 divided by 3 leaves a remainder of 1. However, this simplistic view fails to capture the true essence of the modulo operation.
In its essence, the modulo function is a powerful tool for exploring the concept of congruence in mathematics. Congruence, symbolized by the triple-line notation, relates to the idea of two numbers being equivalent when divided by a common divisor. It's a concept that underpins the foundations of modular arithmetic, a branch of mathematics that finds extensive use in cryptography and computer science.
For example, consider the statement x ≡ y (mod n), where x and y are integers and n is a positive integer known as the modulus. This statement asserts that x and y are congruent modulo n, meaning they have the same remainder when divided by n. In simpler terms, x and y share a special relationship in the context of division by n.
This concept of congruence leads us to uncover the first secret of the modulo function: it serves as a gateway to exploring the fascinating world of modular arithmetic, a realm where numbers behave in unique and often counterintuitive ways.
Practical Tip: Embrace Congruence
To harness the power of the modulo function, it’s essential to understand and embrace the concept of congruence. Here are some practical ways to incorporate congruence into your mathematical toolkit:
- Practice with Basic Congruence Relations: Start with simple examples like x ≡ y (mod 3) and explore the implications. Can you find pairs of numbers that satisfy this relation? What about relations like x ≡ y (mod 10) or x ≡ y (mod 7)?
- Explore Modular Arithmetic Operations: Familiarize yourself with addition, subtraction, multiplication, and even exponentiation in the context of modular arithmetic. For instance, x ≡ 3 (mod 5) and y ≡ 2 (mod 5) means x + y ≡ 0 (mod 5), a powerful tool for solving equations and simplifying expressions.
- Solve Cryptographic Puzzles: Many cryptography challenges involve modular arithmetic. By understanding congruence, you'll be better equipped to tackle these puzzles and unlock the secrets of encrypted messages.
By embracing the concept of congruence, you'll unlock a new dimension of mathematical exploration and gain a deeper appreciation for the modulo function's true potential.
2. Modulo Mastery: Beyond the Basics

While the basic concept of the modulo function is straightforward, its applications can be remarkably diverse and complex. Let’s explore some advanced techniques that will elevate your understanding and mastery of this mathematical tool.
The Euclidean Algorithm: Unraveling GCDs
One of the most powerful applications of the modulo function is in the Euclidean Algorithm, a method for finding the greatest common divisor (GCD) of two integers. This algorithm, attributed to the ancient Greek mathematician Euclid, utilizes repeated application of the modulo operation to identify the largest number that divides two given integers.
The Euclidean Algorithm is a testament to the power of the modulo function, showcasing how this simple operation can lead to profound mathematical insights. By iteratively applying the modulo function, we can efficiently compute GCDs, a fundamental concept in number theory with applications in cryptography, coding theory, and even in understanding the behavior of complex systems.
Here's a simplified version of the Euclidean Algorithm:
- Start with two integers, a and b, where a > b.
- Calculate r1 = a mod b.
- Set a = b and b = r1.
- Repeat steps 2 and 3 until ri = 0.
- The GCD of a and b is the value of b from the previous iteration.
For instance, let's find the GCD of 32 and 18 using the Euclidean Algorithm:
| Iteration | a | b | ri |
|---|---|---|---|
| 1 | 32 | 18 | 14 |
| 2 | 18 | 14 | 4 |
| 3 | 14 | 4 | 2 |
| 4 | 4 | 2 | 0 |
So, the GCD of 32 and 18 is 2.
Practical Tip: GCDs and Modular Arithmetic
The Euclidean Algorithm is a powerful tool for finding GCDs, but its applications extend beyond that. Here’s how you can utilize GCDs in the context of modular arithmetic:
- Solving Linear Congruences: Linear congruences, equations of the form ax ≡ b (mod n), can be solved using the GCD. If a and n are coprime (their GCD is 1), then the equation has a unique solution modulo n. The solution can be found using extended Euclidean Algorithm or other methods.
- Chinese Remainder Theorem (CRT): The CRT is a powerful tool for solving systems of congruences. It allows us to find a solution that satisfies multiple congruences simultaneously. The GCD plays a crucial role in understanding the structure of the solution set and constructing the solution.
- Prime Factorization: The GCD can also be used to identify common factors in numbers, which can aid in prime factorization. Prime factorization is a fundamental concept in number theory and has applications in cryptography and security.
By mastering the Euclidean Algorithm and understanding its applications, you'll gain a powerful toolset for exploring the intricacies of modular arithmetic and its myriad applications.
3. Real-World Applications: Modulo in Action
The modulo function is not just a theoretical concept; it has a wide range of practical applications in various fields. Let’s explore some real-world scenarios where the modulo function plays a crucial role.
Cryptography: Unlocking the Secrets of Secure Communication
Cryptography, the science of secure communication, relies heavily on the principles of modular arithmetic and the modulo function. One of the most famous cryptographic algorithms, the RSA algorithm, is based on the difficulty of factoring large numbers into their prime factors. The modulo function is central to RSA, as it allows for efficient computation of large modular exponentiations, a key component of the algorithm.
In RSA, public and private keys are generated based on the product of two large prime numbers. The security of RSA rests on the assumption that it is computationally infeasible to factor large numbers into their prime factors. The modulo function plays a crucial role in both key generation and encryption/decryption processes.
Computer Science: Beyond Binary
In computer science, the modulo function is a fundamental tool for working with numbers in a finite field. Many computer algorithms, especially those related to data structures and algorithms, utilize modular arithmetic to optimize memory usage and improve computational efficiency.
For instance, hash tables, a common data structure used for efficient data storage and retrieval, rely on the modulo function to map keys to specific indices. The modulo operation ensures that keys are distributed evenly across the table, minimizing collisions and maximizing efficiency.
Practical Tip: Modulo in Everyday Life
While the modulo function may seem like a mathematical curiosity, it has numerous applications in our daily lives. Here are some examples:
- Clock Arithmetic: The 12-hour clock format used in many parts of the world relies on modulo arithmetic. When it's 12:00, the clock resets to 12:00, effectively performing a modulo operation.
- Calendars and Dates: The calendar system we use today is based on modulo arithmetic. Days, weeks, months, and years are all modular units, cycling through a fixed set of values.
- Checksum Verification: Checksum algorithms, used to verify the integrity of data, often involve modular arithmetic. For instance, the Luhn algorithm, used to validate credit card numbers, employs modulo 10 arithmetic to detect errors.
- Image Processing: In digital image processing, the modulo function is used for various operations, such as wrapping pixel values or performing arithmetic operations on color channels.
By recognizing the presence of the modulo function in everyday applications, you'll gain a deeper appreciation for its versatility and importance.
Conclusion: Unlocking the Secrets of the Modulo Function
The modulo function, a simple yet powerful tool, holds a wealth of secrets and applications that extend far beyond basic remainder calculations. By exploring the concept of congruence, mastering advanced techniques like the Euclidean Algorithm, and understanding its real-world applications, we’ve uncovered the true potential of this mathematical concept.
Whether you're a mathematician, computer scientist, or just an enthusiast, the modulo function offers a fascinating journey into the world of number theory and its practical applications. By embracing the secrets of the modulo function, you'll gain a powerful toolkit for exploring the intricate relationships between numbers and unlocking the mysteries of modular arithmetic.
So, let the modulo function be your guide as you navigate the fascinating world of mathematics and computer science. With these three tips, you're well on your way to becoming a modulo master!
How is the modulo function used in programming languages?
+The modulo function, often denoted as %, is a fundamental operator in most programming languages. It is used for various purposes, including calculating remainders, implementing congruence relations, and performing operations in finite fields. In programming, the modulo operation is especially useful for checking if a number is even or odd, generating random numbers within a specific range, and implementing algorithms that rely on modular arithmetic.
What are some real-world applications of modular arithmetic besides cryptography and computer science?
+Modular arithmetic has a wide range of applications beyond cryptography and computer science. It is used in music theory to analyze rhythms and musical structures, in game theory for solving certain types of games, in finance for calculating interest rates and loan payments, and in various fields of science for modeling periodic phenomena.
How can I practice my understanding of the modulo function and modular arithmetic?
+There are several ways to practice and enhance your understanding of the modulo function and modular arithmetic. You can start by solving mathematical puzzles and problems that involve modular arithmetic. Websites like Project Euler and Brilliant offer a variety of challenging problems that utilize modular arithmetic. Additionally, you can explore online courses and tutorials specifically focused on modular arithmetic and its applications.