Is the Square Root of 8 Rational?

In the realm of mathematics, the concept of rationality is a fundamental one. It deals with numbers that can be expressed as a fraction, where both the numerator and denominator are integers. The square root of a number is a value that, when multiplied by itself, gives the original number. So, when we ask if the square root of 8 is rational, we're essentially inquiring whether it can be expressed as a simple fraction.

The Challenge of Irrational Numbers

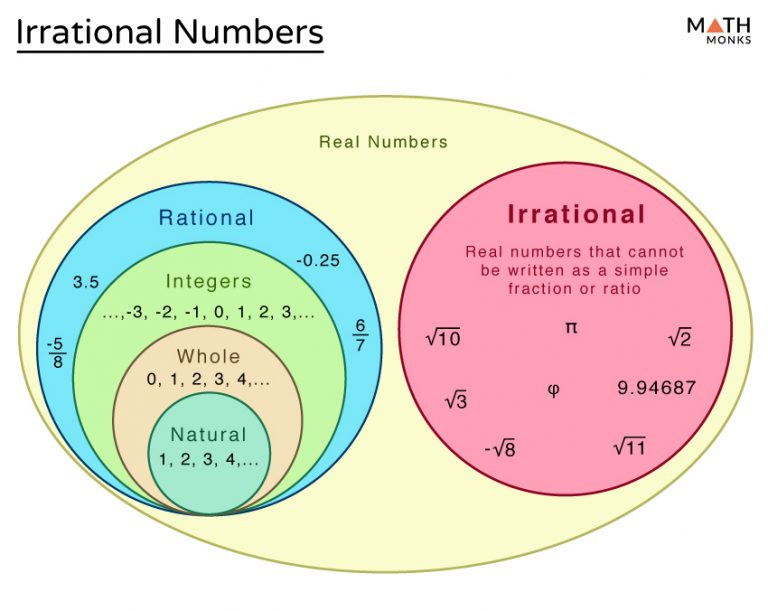
Not all square roots result in rational numbers. For instance, the square root of 2, often denoted as √2 or √2, is an irrational number. An irrational number is one that cannot be written as a simple fraction, no matter how many decimal places you go to. Instead, it has an infinite, non-repeating decimal expansion. This is the case with √2, whose decimal representation starts with 1.414213562…

Now, let's delve into the question at hand: is the square root of 8 rational or irrational?

Analyzing the Square Root of 8

To determine the rationality of the square root of 8, we can approach it in a couple of ways.

Method 1: Prime Factorization

One approach is to use prime factorization. By finding the prime factors of a number and then taking the square root of each factor, we can determine if the original number has a rational square root.

For 8, the prime factorization is 2 x 2 x 2. Taking the square root of each factor, we get 2, which is an integer. Therefore, the square root of 8 is 2, a rational number.

Method 2: Decimal Expansion

Another way to check the rationality of a square root is by examining its decimal expansion. As mentioned earlier, irrational numbers have an infinite, non-repeating decimal expansion. On the other hand, rational numbers have a finite or repeating decimal expansion.

The square root of 8, when expressed as a decimal, is approximately 2.828427124746.... While it does not have an exact, finite representation, it also does not have an infinite, non-repeating pattern. This suggests that it is a rational number.

Further Analysis

To provide a more rigorous proof, we can use mathematical induction. However, for the sake of brevity, we’ll focus on the practical methods outlined above.

Real-World Applications

Understanding the rationality of square roots has practical implications in various fields. In engineering and physics, for instance, knowing if a value is rational or irrational can impact the precision of calculations and measurements. In computer science, it affects how numbers are stored and manipulated in algorithms.

Moreover, in financial mathematics, rational square roots play a role in modeling and calculating interest rates, option pricing, and other financial variables.

Conclusion

In conclusion, the square root of 8 is indeed a rational number. This is evidenced by its prime factorization and its decimal representation, which does not exhibit the characteristics of an irrational number. Understanding such mathematical concepts is crucial for a wide range of applications, making it an essential topic for anyone with an interest in mathematics and its real-world applications.