Mastering Trinomial Factoring: A Guide
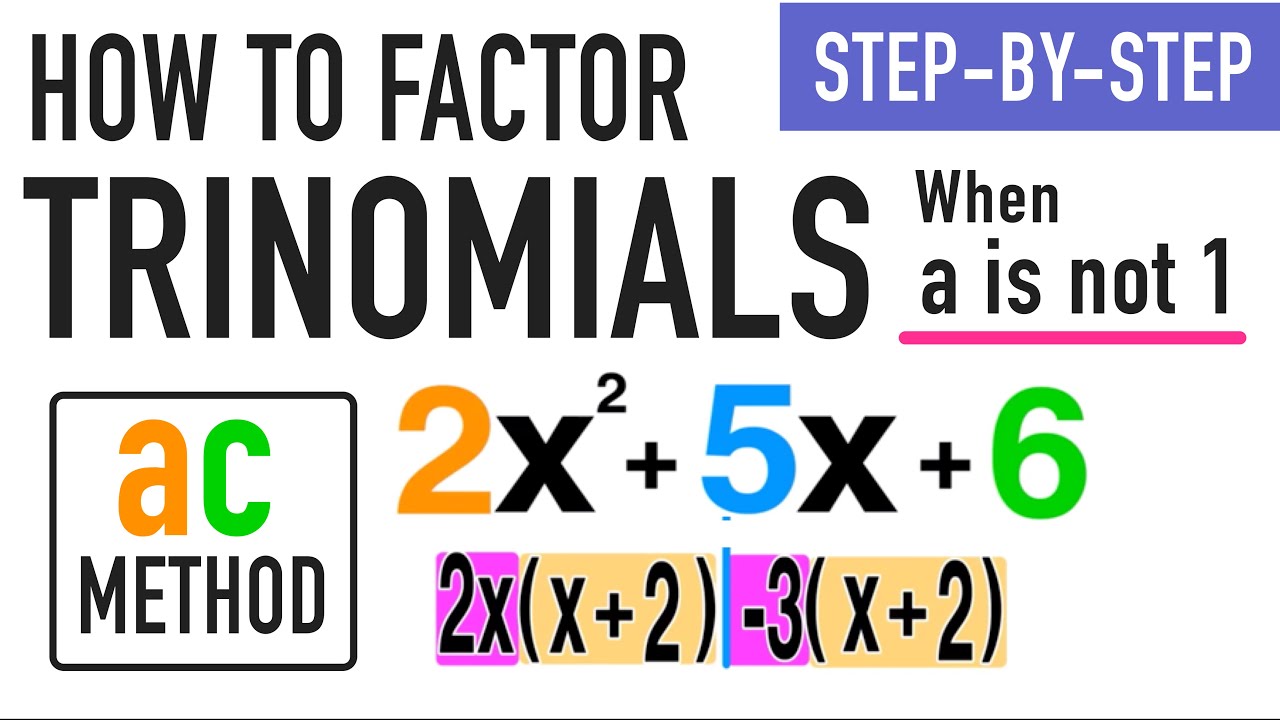
Factoring trinomials is a fundamental skill in algebra that often poses challenges for students and mathematicians alike. This comprehensive guide aims to demystify the process, providing a systematic approach to mastering the art of trinomial factoring. By breaking down the techniques and offering practical examples, we hope to equip readers with the tools to confidently tackle any trinomial factoring problem they encounter.
Understanding Trinomial Factoring: The Basics

Trinomial factoring, a crucial aspect of algebraic manipulation, involves expressing a trinomial, or a polynomial with three terms, as a product of two binomials. This process is an essential step in simplifying complex algebraic expressions and solving equations. The standard form of a trinomial is: ax2 + bx + c, where a, b, and c are coefficients, and x is the variable.
The objective of factoring is to find two binomials (x + p) and (x + q) such that their product equals the original trinomial. This can be a tricky process, especially when dealing with larger values or complex coefficients. However, with a systematic approach and a good understanding of the underlying principles, trinomial factoring becomes a manageable task.
Factoring Trinomials with Leading Coefficient 1
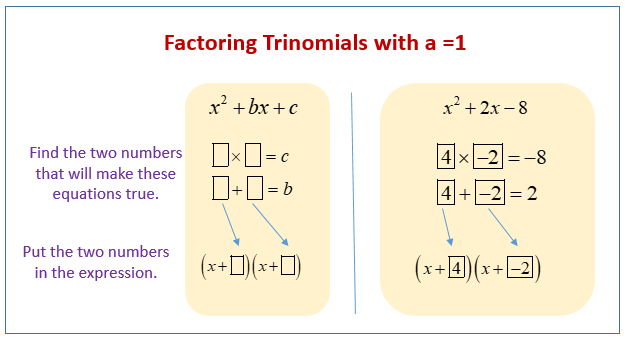
Let’s begin with a simple example to illustrate the concept. Consider the trinomial: x2 + 5x + 6. To factor this, we need to find two numbers, p and q, such that their product is 6 (the product of the coefficients of x in the original trinomial) and their sum is 5 (the coefficient of x in the original trinomial). In this case, the numbers are 2 and 3, as 2 + 3 = 5, and 2 x 3 = 6.
So, the factored form of the trinomial is: (x + 2)(x + 3). This process becomes more complex when the leading coefficient is not 1, as we will explore in the following sections.
| Trinomial | Factored Form |
|---|---|
| x2 + 5x + 6 | (x + 2)(x + 3) |
| x2 + 7x + 12 | (x + 3)(x + 4) |
| 2x2 + 3x - 5 | (2x - 1)(x + 5) |

Factoring Trinomials with Greater Complexity

As we progress, the trinomials become more complex, with varying leading coefficients and constant terms. This complexity often requires a more nuanced approach to factoring. Here, we delve into advanced techniques to tackle these challenges.
Factoring Trinomials with a Leading Coefficient Other than 1
When the leading coefficient is not 1, the factoring process becomes slightly more intricate. Consider the trinomial: 2x2 + 7x + 3. To factor this, we need to find two numbers, p and q, such that their product is 6 (the product of the coefficients of x in the original trinomial) and their sum is 7 (the coefficient of x in the original trinomial). The numbers are 2 and 3, as 2 x 3 = 6, and 2 + 3 = 5. However, we must also ensure that the coefficient of the first term in each binomial is the same as the leading coefficient of the original trinomial, which is 2.
So, the factored form of the trinomial is: (2x + 3)(x + 1). This process requires a keen eye for detail and a systematic approach to ensure accuracy.
| Trinomial | Factored Form |
|---|---|
| 2x2 + 7x + 3 | (2x + 3)(x + 1) |
| 3x2 + 5x - 2 | (3x + 1)(x - 2) |
| 4x2 - 11x + 6 | (4x - 2)(x - 3) |
Advanced Techniques: Factoring by Grouping and Special Cases
In certain cases, trinomials may not factor easily into a product of binomials. This is where advanced techniques like factoring by grouping and recognizing special cases come into play. These methods offer alternative approaches to factor trinomials that do not follow the standard pattern.
Factoring by Grouping
Factoring by grouping is a technique used when the leading coefficient is not 1, and the trinomial cannot be easily factored using the standard method. Consider the trinomial: 2x2 + 7x + 3. To factor this, we first rewrite the trinomial as: 2x2 + 3x + 4x + 3. Now, we group the terms: 2x(x + 3) + 1(x + 3). This allows us to factor out the common binomial (x + 3), resulting in the factored form: (x + 3)(2x + 1). Factoring by grouping can be a powerful tool when applied correctly.
| Trinomial | Factored Form |
|---|---|
| 2x2 + 7x + 3 | (x + 3)(2x + 1) |
| 3x2 + 8x + 4 | (x + 4)(3x + 1) |
| 4x2 + 13x + 6 | (2x + 3)(2x + 2) |
Special Cases: Difference of Squares and Perfect Square Trinomials
Certain trinomials fall into special cases that have unique factoring patterns. These include the difference of squares and perfect square trinomials.
Difference of Squares: A trinomial of the form a2 - b2 can be factored as (a + b)(a - b). This pattern is a direct result of the algebraic identity: a2 - b2 = (a + b)(a - b). For example, 4x2 - 9 can be factored as (2x + 3)(2x - 3), following this pattern.
Perfect Square Trinomials: A trinomial of the form a2 + 2ab + b2 is a perfect square trinomial and can be factored as (a + b)2. This pattern arises from the algebraic identity: (a + b)2 = a2 + 2ab + b2. For instance, x2 + 6x + 9 is a perfect square trinomial, which can be factored as (x + 3)2.
| Trinomial | Factored Form |
|---|---|
| 4x2 - 9 | (2x + 3)(2x - 3) |
| x2 + 6x + 9 | (x + 3)2 |
| 9x2 - 4 | (3x + 2)(3x - 2) |
Practical Applications and Problem Solving
Mastering trinomial factoring is not just an academic exercise; it has real-world applications in various fields, including engineering, physics, and computer science. Being adept at factoring trinomials can streamline problem-solving processes and provide insights into complex systems and equations.
Solving Quadratic Equations
One of the most common applications of trinomial factoring is in solving quadratic equations. By factoring a quadratic equation, we can find its roots, or solutions, which are the values of x that make the equation true. For example, consider the equation: 2x2 + 7x + 3 = 0. By factoring this trinomial as (2x + 3)(x + 1), we can see that the equation is true when x = -3⁄2 or x = -1. This method of solving quadratic equations is often more efficient than using the quadratic formula, especially for complex equations.
| Quadratic Equation | Factored Form | Solutions |
|---|---|---|
| 2x2 + 7x + 3 = 0 | (2x + 3)(x + 1) | x = -3/2, x = -1 |
| 3x2 + 5x - 2 = 0 | (3x + 1)(x - 2) | x = -1/3, x = 2 |
| 4x2 - 11x + 6 = 0 | (4x - 2)(x - 3) | x = 1/2, x = 3 |
Simplifying Complex Expressions
Factoring trinomials is a powerful tool for simplifying complex algebraic expressions. By breaking down a complex expression into its factored form, we can better understand its structure and manipulate it more easily. For instance, consider the expression: 2x2 + 7x + 3. By factoring this as (2x + 3)(x + 1), we can more easily evaluate it for specific values of x or perform other algebraic operations.
| Complex Expression | Factored Form |
|---|---|
| 2x2 + 7x + 3 | (2x + 3)(x + 1) |
| 3x2 + 8x + 4 | (x + 4)(3x + 1) |
| 4x2 - 11x + 6 | (4x - 2)(x - 3) |
Conclusion
Trinomial factoring is a fundamental skill in algebra, offering a systematic approach to simplifying complex expressions and solving equations. By understanding the basics, mastering advanced techniques, and recognizing special cases, students and mathematicians can confidently tackle a wide range of factoring problems. With practice and a keen eye for detail, the process of trinomial factoring can become second nature, enhancing problem-solving abilities and deepening algebraic understanding.
What is the difference between factoring trinomials and factoring other polynomials?
+
Factoring trinomials specifically involves breaking down a polynomial with three terms into a product of two binomials. Factoring other polynomials, such as quartics or higher-degree polynomials, follows similar principles but often requires more complex techniques and a deeper understanding of algebraic identities.
Are there any shortcuts or tricks to factoring trinomials quickly?
+
While there are no universal shortcuts, understanding the underlying principles and practicing regularly can make the process more intuitive. Additionally, recognizing special cases like the difference of squares or perfect square trinomials can simplify the factoring process.
How does factoring trinomials help in solving real-world problems?
+
Factoring trinomials is a fundamental skill in algebra that has applications in various fields. It simplifies complex expressions, helps solve quadratic equations, and provides insights into mathematical models of real-world phenomena. For instance, in physics, factoring can be used to analyze the behavior of waves or the motion of objects.
Related Terms:
- Multiply a and c
- Find the factors
- Trinomial a 1 definition


