An Irrational Number Count: Unveiling the Mystery

In the realm of mathematics, where precision and logic reign supreme, there exists a fascinating category of numbers known as irrational numbers. These enigmatic values, which cannot be expressed as a simple fraction, have captivated mathematicians and enthusiasts alike for centuries. The quest to uncover the secrets of irrational numbers is an ongoing adventure, and in this article, we delve into the depths of their mystery, exploring their characteristics, significance, and the unique role they play in the mathematical universe.
The Nature of Irrational Numbers
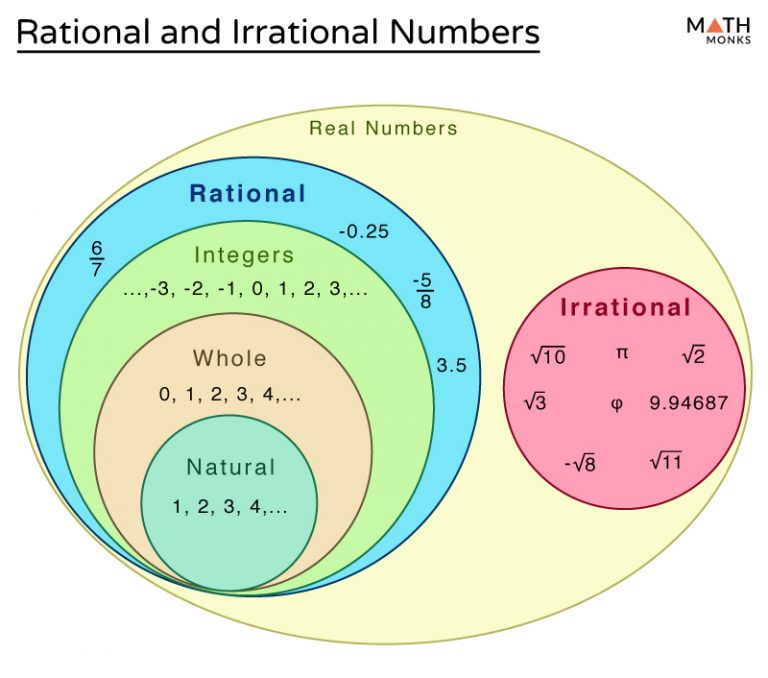
Irrational numbers are a peculiar breed, defying the conventional definition of a number. Unlike rational numbers, which can be written as a ratio of two integers, irrational numbers have an infinite and non-repeating decimal expansion. This infinite nature sets them apart and adds an element of intrigue to their study.
One of the most iconic irrational numbers is π (pi), the mathematical constant that represents the ratio of a circle's circumference to its diameter. With an infinite decimal expansion that begins with 3.14159..., π is a prime example of an irrational number. Its irrationality has profound implications in various fields, from geometry to physics.
Another well-known irrational number is e, also known as Euler's number. With a value of approximately 2.71828..., e plays a crucial role in exponential functions and is fundamental in fields like calculus and complex analysis.
While π and e are perhaps the most famous irrational numbers, they are not alone. The set of irrational numbers is incredibly vast, encompassing an infinite array of values. From the square root of 2 (approximately 1.41421...) to the golden ratio (approximately 1.61803...), irrational numbers permeate the mathematical landscape.
Historical Context and Discovery
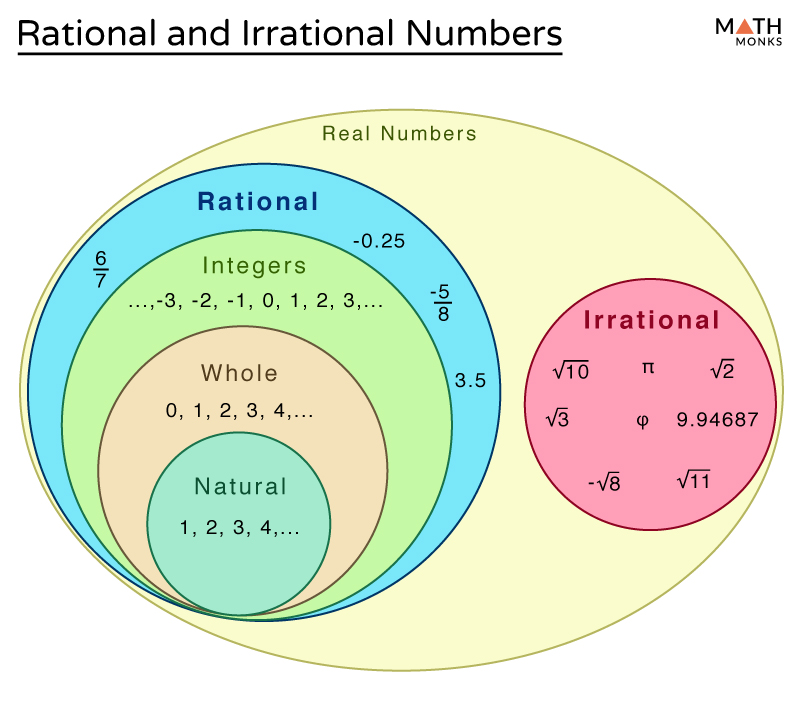
The concept of irrational numbers has a rich historical backdrop, dating back to ancient civilizations. The Greeks, particularly the mathematician Pythagoras, encountered irrational numbers while studying geometric proportions. The discovery of irrationality in the square root of 2 is often attributed to Pythagoras, who, according to legend, kept this knowledge a secret, fearing it might disrupt the harmony of the universe.
Over time, mathematicians grappled with the existence of irrational numbers, developing theories and proofs to understand their nature. The work of mathematicians like Euclid and Archimedes contributed significantly to our understanding of irrationals. Their efforts laid the foundation for further exploration and the development of mathematical theories that accommodate these unique numbers.
Applications and Significance
Irrational numbers may seem abstract, but their impact on various fields is profound. In physics, π and e are fundamental constants that govern the behavior of physical systems. In engineering, irrational numbers play a crucial role in designing complex structures and calculating precise measurements.
One of the most remarkable applications of irrational numbers is in the field of cryptography. The security of modern encryption algorithms often relies on the complexity of prime factorization, a process that involves irrational numbers. The unique properties of irrationals make them invaluable in ensuring the confidentiality of sensitive information.
In the realm of pure mathematics, irrational numbers have inspired the development of advanced number systems and theories. The study of transcendental numbers, a subset of irrationals, has led to profound insights into the nature of numbers and the limits of mathematical proof.
Mathematical Properties and Proofs
Irrational numbers possess unique properties that set them apart from rational numbers. One of the fundamental properties is their density in the number line. Unlike rational numbers, which are separated by gaps, irrational numbers fill the spaces between rationals, creating a continuous spectrum.
The proof of irrationality for specific numbers is a fascinating aspect of mathematics. One classic proof involves demonstrating that the square root of 2 is irrational. This proof, often attributed to the Greek mathematician Hippasus, is a testament to the early understanding of irrational numbers.
Another notable proof is the proof of irrationality for the golden ratio, a number that appears in various natural phenomena and artistic compositions. The elegant proof, which involves the Fibonacci sequence, showcases the beauty and complexity of mathematical reasoning.
| Irrational Number | Decimal Expansion |
|---|---|
| π | 3.141592653589793... |
| e | 2.718281828459045... |
| Golden Ratio | 1.618033988749895... |

The Beauty of Irrationals
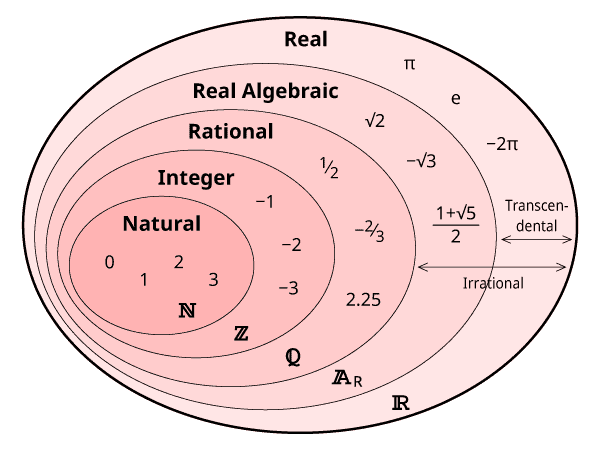
Beyond their mathematical significance, irrational numbers possess an inherent beauty. The infinite and unpredictable nature of their decimal expansions adds an artistic touch to the cold logic of mathematics. The concept of irrationality challenges our perception of order and symmetry, inviting us to explore the intricacies of the mathematical universe.
Irrational numbers have inspired artists, musicians, and poets, who find beauty in the unpredictable and infinite. From the intricate patterns of fractals to the rhythmic beats of music, the influence of irrational numbers extends beyond the boundaries of mathematics.
Future Prospects and Open Questions
While we have made significant strides in understanding irrational numbers, many mysteries remain. The study of irrationals continues to push the boundaries of mathematical knowledge, with researchers exploring new theories and applications.
One area of ongoing research is the exploration of irrational numbers in higher dimensions. Mathematicians are investigating the behavior of irrational numbers in complex spaces, seeking to uncover new patterns and connections.
Additionally, the study of irrational numbers in the context of quantum mechanics and theoretical physics offers exciting possibilities. The unique properties of irrationals may hold the key to unlocking new insights into the fundamental nature of the universe.
Conclusion
In the vast landscape of mathematics, irrational numbers stand as a testament to the endless curiosity and ingenuity of the human mind. Their infinite nature and enigmatic behavior have captivated mathematicians and enthusiasts for millennia. From the ancient Greeks to modern-day researchers, the study of irrational numbers continues to inspire and challenge, driving us to explore the uncharted territories of mathematical discovery.
How are irrational numbers used in real-world applications?
+Irrational numbers find applications in various fields. In physics, they are crucial in understanding the behavior of particles and waves. In engineering, they are used for precise calculations and designs. Cryptography relies on the complexity of irrational numbers for secure encryption.
What is the significance of the golden ratio in art and design?
+The golden ratio, an irrational number, is believed to possess aesthetic appeal and harmony. Artists and designers often use it to create visually pleasing compositions, as it is thought to reflect the natural proportions found in the universe.
Are there any practical ways to approximate irrational numbers?
+Yes, while irrational numbers have infinite decimal expansions, they can be approximated to a desired level of precision. For example, π can be approximated as 3.14, which is sufficient for many calculations. However, for more precise work, higher decimal places are required.