The Simple Guide to Averaging Percentages

Calculating the average of percentages can seem daunting, especially when dealing with complex data sets or multiple variables. However, with a systematic approach and a few simple formulas, you can easily find the mean percentage with confidence. In this guide, we will demystify the process, break down the necessary steps, and provide practical examples to help you master the art of averaging percentages.

Understanding the Basics: Percentage, Average, and Their Relationship

A percentage is a way to express a number as a fraction of 100. It is a fundamental concept in mathematics and is widely used in various fields, including finance, statistics, and everyday life. When we talk about averaging percentages, we are essentially finding the central tendency of a set of percentages, which provides valuable insights into the overall trend or behavior of the data.

The average, also known as the mean, is a measure of central tendency that represents the typical or common value in a dataset. In the context of percentages, the average percentage tells us the "average strength" or "typical proportion" of a particular quantity relative to the whole.

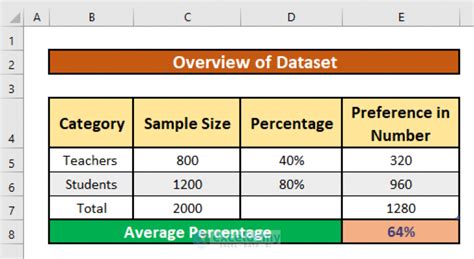
Mathematically, the average percentage, denoted as AP, can be calculated using the following formula:

AP = (P1 + P2 + ... + Pn) / n

where P1, P2, ..., Pn represent the individual percentages, and n is the total number of percentages in the dataset.

For example, let's consider a simple scenario: you have a group of five students, and you want to find the average percentage of their exam scores. If their scores are 85%, 90%, 78%, 92%, and 88%, the average percentage can be calculated as follows:

AP = (85 + 90 + 78 + 92 + 88) / 5 = 433 / 5 = 86.6%

So, the average percentage of their exam scores is 86.6%, indicating that, on average, the students scored around 86.6% on the exam.

Dealing with Different Types of Percentages

When averaging percentages, it’s crucial to recognize that percentages can take on different forms and represent various quantities. Understanding these differences is essential for accurate calculations.

1. Whole Percentages

Whole percentages are the most common type, representing a value out of 100. These percentages are straightforward and easy to work with when averaging. For instance, if you have a dataset with whole percentages like 30%, 45%, and 25%, the average can be directly calculated as (30 + 45 + 25) / 3 = 100 / 3 = 33.33%.

2. Percentage Points

Percentage points, often denoted as pp, represent a change or difference in percentages. They are used to express the magnitude of change, rather than an absolute value. For example, if a stock price increases from 10% to 15%, the change is 5 pp (15 - 10 = 5). When averaging percentage points, ensure you are working with the actual change values rather than the original percentages.

3. Percentage Change

Percentage change, denoted as %Δ, represents the relative change between two values. It is calculated using the formula: %Δ = ((Final Value - Initial Value) / Initial Value) * 100. For instance, if a population increases from 1000 to 1200, the percentage change is ((1200 - 1000) / 1000) * 100 = 20%. When averaging percentage changes, ensure you are working with the relative changes rather than the absolute values.

Advanced Techniques: Weighted Average and Percentages

In some cases, the percentages you are dealing with may not carry equal importance or weight. This is where the concept of a weighted average comes into play. A weighted average assigns different weights to each percentage based on its significance or contribution. The formula for calculating the weighted average percentage, WAP, is as follows:

WAP = (w1 * P1 + w2 * P2 + ... + wn * Pn) / (w1 + w2 + ... + wn)

where w1, w2, ..., wn represent the weights assigned to each percentage, and P1, P2, ..., Pn are the individual percentages.

For example, let's say you have a survey with two questions, and you want to find the average percentage of positive responses. Question 1 has a weight of 0.6 (indicating higher importance), and Question 2 has a weight of 0.4. The responses for Question 1 are 70% positive, and for Question 2, they are 85% positive. The weighted average percentage can be calculated as follows:

WAP = (0.6 * 70 + 0.4 * 85) / (0.6 + 0.4) = 79%

So, the weighted average percentage of positive responses is 79%, reflecting the importance of each question in the survey.

Averting Common Pitfalls: Tips for Accurate Calculations

Avoiding common mistakes is crucial when working with percentages and averages. Here are some tips to ensure accurate calculations:

• Check Your Data: Always double-check your data for accuracy and consistency. Ensure that the percentages are correctly calculated and represented.
• Convert to Decimal: When dealing with complex calculations or formulas, it's often easier to convert percentages to decimals. Simply divide the percentage by 100. For instance, 30% becomes 0.30.
• Watch Out for Signs: Be mindful of positive and negative signs when calculating percentage changes. A negative change indicates a decrease, while a positive change represents an increase.
• Use Online Tools: For more complex scenarios or to verify your calculations, consider using online percentage calculators or statistical software. These tools can provide additional insights and accuracy.

Applying Average Percentages in Real-World Scenarios

Average percentages have numerous applications in various fields. Here are a few examples:

• Business and Finance: Average percentages are used to calculate return on investment (ROI), profit margins, and sales growth rates. They help businesses assess their financial performance and make informed decisions.
• Education: Teachers and educators use average percentages to evaluate student performance, track progress, and identify areas for improvement.
• Health and Fitness: In the healthcare industry, average percentages are used to monitor patient recovery rates, track obesity levels, and assess the effectiveness of treatments.
• Social Sciences: Average percentages are employed in surveys and polls to understand public opinion, voting trends, and demographic patterns.

Visualizing Average Percentages: Graphs and Charts

Visual representations, such as graphs and charts, can greatly enhance the understanding and interpretation of average percentages. Here are some commonly used visual tools:

• Bar Graphs: Bar graphs are excellent for comparing average percentages across different categories or time periods. Each bar represents a category, and the height of the bar corresponds to the average percentage.
• Line Graphs: Line graphs are useful for visualizing trends and changes in average percentages over time. The x-axis represents time, and the y-axis represents the average percentage.
• Pie Charts: Pie charts are ideal for showing the composition or breakdown of a whole. Each slice of the pie represents a category, and the angle of the slice corresponds to the average percentage of that category.

By using visual representations, you can communicate complex data in a simple and intuitive manner, making it easier for stakeholders to grasp the insights and take informed actions.

Conclusion: Mastering the Art of Averaging Percentages

Averaging percentages is a valuable skill that empowers you to make informed decisions and draw meaningful conclusions from data. By understanding the basics, dealing with different types of percentages, and applying advanced techniques like weighted averages, you can tackle a wide range of real-world scenarios. Remember to always double-check your calculations, convert percentages to decimals when needed, and utilize visual representations to enhance your analysis.

With practice and a systematic approach, you'll become proficient in calculating average percentages, unlocking a deeper understanding of data and its implications. So, embrace the power of percentages, and let your insights guide you toward success in your endeavors!