Understanding Negative Numbers: Greater Than or Less Than?
The concept of negative numbers can often be a source of confusion for those new to mathematics or even for individuals revisiting the topic. The rules governing negative numbers are fundamental to arithmetic and algebra, making it crucial to grasp the distinction between negative numbers that are greater than or less than zero.
This article aims to demystify negative numbers, offering a comprehensive understanding of their position in the number line and their relative values. By exploring the intricacies of negative numbers, we can develop a stronger foundation for more complex mathematical concepts.
The Basics: Positive and Negative Numbers

In mathematics, numbers can be broadly categorized into two main types: positive and negative. Positive numbers are the ones we typically encounter in everyday life, representing quantities such as height, temperature, or countable objects. They are denoted by whole numbers or decimals greater than zero.
Negative numbers, on the other hand, represent values less than zero. They are often associated with deficits, losses, or distances below a reference point. Negative numbers are identified by the presence of a minus sign (−) before the numerical value.
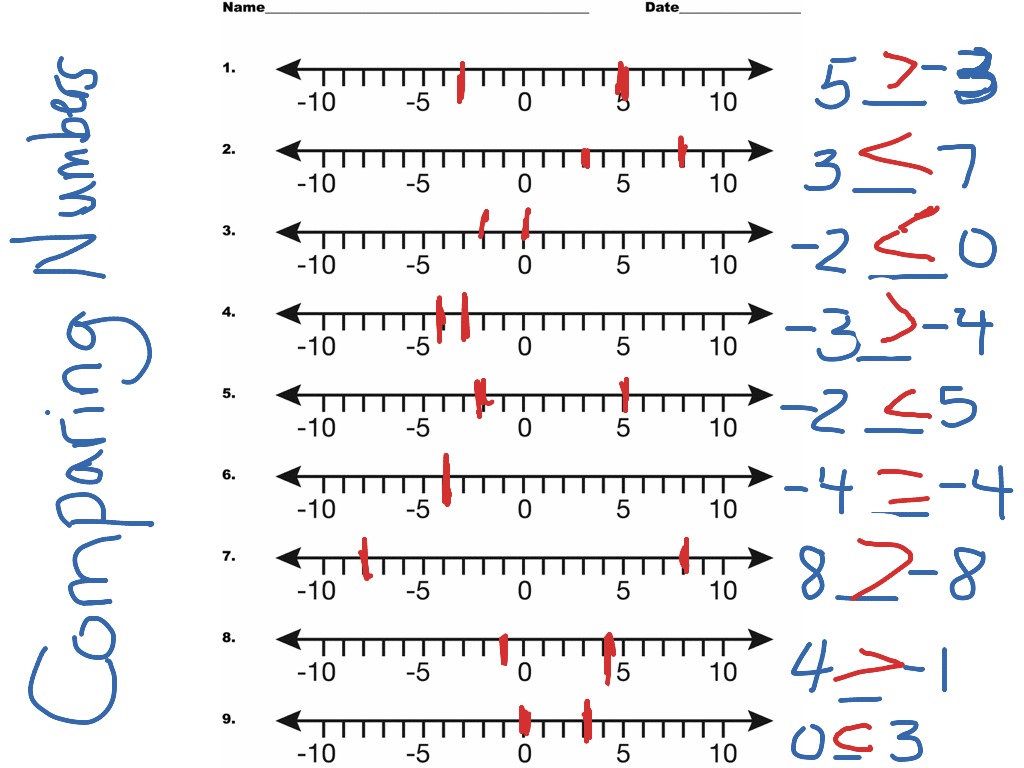
The number line provides a visual representation of the relationship between positive and negative numbers. It extends infinitely in both directions, with zero as the reference point. To the left of zero, we find negative numbers, and to the right, positive numbers.
| Number Type | Examples |
|---|---|
| Positive Numbers | 1, 2.5, 100, π |
| Negative Numbers | −3, −0.75, −20 |

The Magnitude of Negative Numbers
The magnitude of a negative number refers to its absolute value, ignoring the negative sign. For example, the magnitude of −5 is 5, as both numbers represent the same distance from zero on the number line, but in opposite directions.
When comparing the magnitude of negative numbers, we follow the same rules as for positive numbers. A larger magnitude indicates a greater distance from zero, regardless of the sign. For instance, −8 has a larger magnitude than −3, as it represents a further distance to the left on the number line.
The Sign of Negative Numbers
The sign of a number indicates its position relative to zero on the number line. Negative numbers have a minus sign (−) before their numerical value, indicating that they are less than zero.
The sign of a negative number is crucial when performing arithmetic operations. For example, when adding two negative numbers, the result is also negative. Similarly, subtracting a positive number from a negative number yields a larger negative value.
Comparing Negative Numbers: Greater Than or Less Than

Comparing negative numbers involves assessing their position on the number line relative to zero and to each other. This comparison determines whether one negative number is greater than, less than, or equal to another.
The Number Line Approach
One intuitive way to compare negative numbers is by visualizing them on the number line. Negative numbers are to the left of zero, and their distance from zero increases as the magnitude of the negative number increases.
When comparing two negative numbers, we can determine which is greater by observing their position on the number line. The number that is further to the left is the larger negative number, as it has a greater magnitude.
Using Inequality Symbols
Inequality symbols are used to express the relationship between two numbers. In the context of negative numbers, these symbols help us determine whether one number is greater than (>), less than (<), or equal to (=) another.
| Comparison | Inequality Symbol | Explanation |
|---|---|---|
| −5 > −3 | > | −5 is greater than −3 because it has a larger magnitude and is further to the left on the number line. |
| −2 < −8 | < | −2 is less than −8 as it has a smaller magnitude and is closer to zero on the number line. |
| −7 = −7 | = | −7 is equal to itself, as the magnitude and position on the number line remain the same. |
Absolute Value and Comparison
The absolute value of a number is its magnitude, regardless of its sign. When comparing negative numbers, we can use absolute values to determine their relative sizes.
If the absolute values of two negative numbers are different, the negative number with the larger absolute value is considered greater. For instance, −6 is greater than −4 because |−6| = 6 is larger than |−4| = 4.
Rules for Comparing Negative Numbers
To establish a consistent approach for comparing negative numbers, several rules can be followed:
- If the absolute values of two negative numbers are equal, the numbers are also equal.
- If the absolute values of two negative numbers are different, the number with the larger absolute value is greater.
- When comparing negative numbers with the same absolute value, the number with the minus sign closer to the left is greater.
Examples of Comparison
Let’s apply these rules to some examples:
- −5 > −3 because the absolute value of −5 is larger.
- −2 < −8 as the absolute value of −8 is greater.
- −7 = −7 since the absolute values are equal.
- −10 > −10.5 despite having the same absolute value, −10 is greater due to its minus sign being closer to the left.
Applications and Real-World Examples
Understanding the concept of negative numbers and their comparison is essential in various mathematical and real-world scenarios.
Algebra and Equations
In algebra, negative numbers are fundamental for solving equations and understanding the behavior of functions. They allow us to model situations involving losses, debts, or distances below a reference point.
Financial Transactions
In finance, negative numbers are used to represent debts, expenses, or losses. For example, a negative balance in a bank account indicates an overdrawn amount, and understanding the comparison of negative numbers helps in financial planning and budgeting.
Temperature Measurements
Negative numbers are commonly used to represent temperatures below zero. For instance, −10°C is a colder temperature than −5°C, as the magnitude of −10 is larger.
Tips for Mastering Negative Numbers

Grasping the concept of negative numbers and their comparison can be challenging, but with practice and a solid understanding of the number line, it becomes easier.
- Visualize the number line: Use the number line as a reference to compare negative numbers and their positions relative to zero.
- Practice with examples: Solve various comparison problems involving negative numbers to reinforce your understanding.
- Understand the rules: Familiarize yourself with the rules for comparing negative numbers to ensure consistent and accurate comparisons.
- Apply in real-world contexts: Relate negative numbers to real-life scenarios, such as temperatures or financial transactions, to enhance your comprehension.
FAQ
Can a negative number be greater than a positive number?
+No, a negative number cannot be greater than a positive number. Positive numbers have values greater than zero, while negative numbers are less than zero. When comparing a negative number to a positive number, the positive number will always be greater.
Are negative numbers always smaller than positive numbers?
+Yes, negative numbers are always smaller than positive numbers. The minus sign (−) indicates a value less than zero, while positive numbers are greater than zero. Therefore, negative numbers have smaller magnitudes compared to positive numbers.
How can I compare two negative numbers with the same absolute value?
+When two negative numbers have the same absolute value, you can compare them by looking at their position on the number line. The number with the minus sign closer to the left is considered greater. For example, −10 is greater than −10.5 despite having the same absolute value.



