Excel Function: How to Sin in Degrees
The Excel SIN function is a mathematical formula used to calculate the sine of an angle. While it is primarily used for angles in radians, Excel also provides the option to work with angles in degrees. This feature is especially useful for those who are more familiar with degree measurements or when dealing with real-world applications where degrees are commonly used, such as in geography, architecture, or engineering.
Understanding the SIN Function in Excel

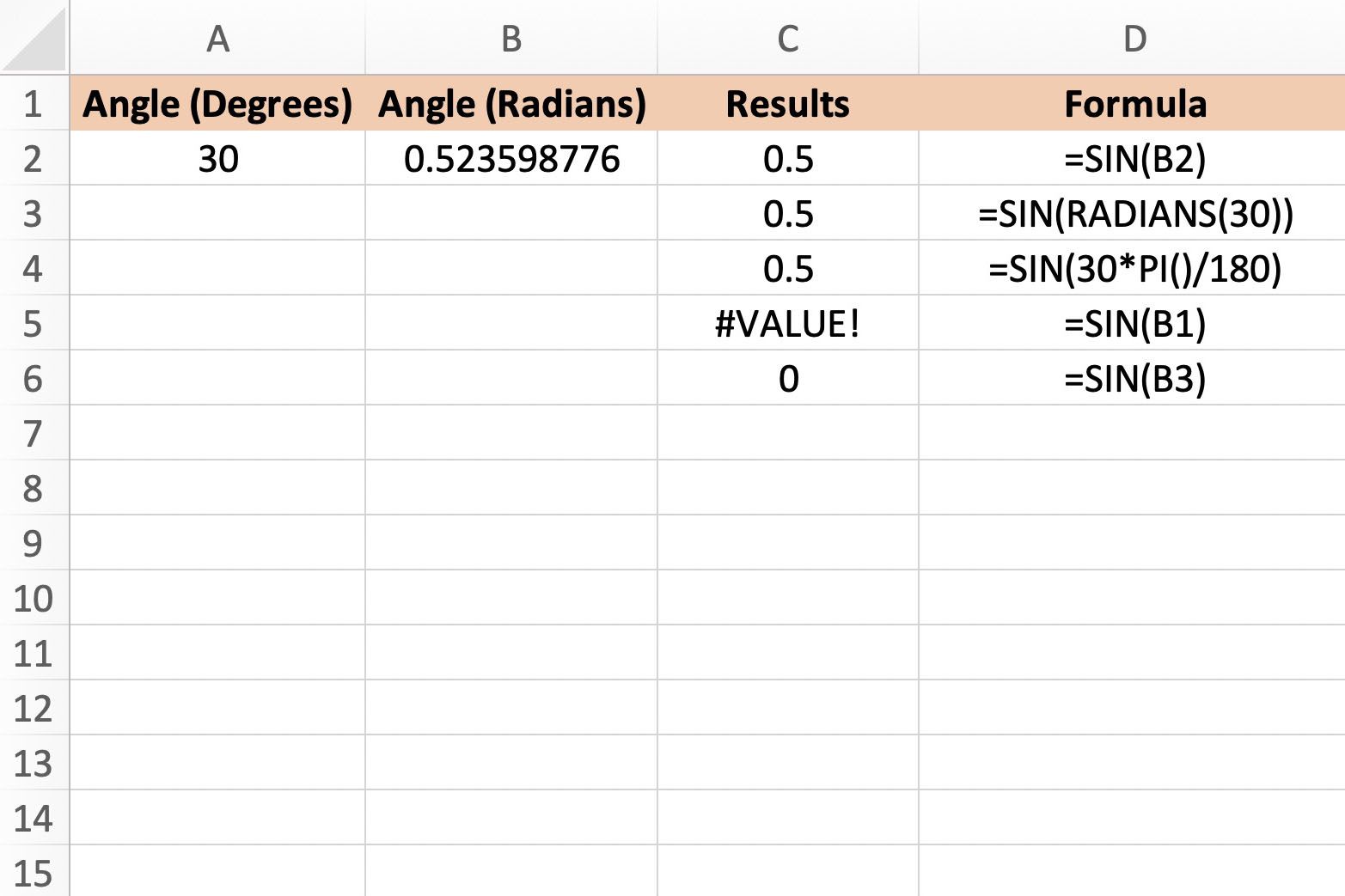
The SIN function in Excel is a simple yet powerful tool for trigonometric calculations. It returns the sine of an angle, which is one of the basic trigonometric functions. The formula for the SIN function is =SIN(angle), where angle represents the angle for which you want to find the sine.
By default, Excel assumes angles are in radians. However, it provides a built-in feature to easily switch between radians and degrees. This flexibility makes it convenient for users to work with angles in their preferred unit of measurement.
Switching Between Radians and Degrees
To use the SIN function with angles in degrees, you need to ensure that the Calculation Options in Excel are set to Degrees. Here’s how you can do it:
- Click on the File tab in the Excel ribbon.
- Select Options from the left-hand menu.
- In the Excel Options dialog box, navigate to the Formulas category.
- Under the Working with formulas section, look for the Calculation options field.
- Ensure that the Degrees option is selected. If it isn't, choose it from the dropdown menu.
- Click OK to save the changes.
Now, when you use the SIN function, Excel will interpret the angle as degrees. This setting remains active until you change it back to radians or another unit.
Using the SIN Function with Degrees
Once you’ve set the calculation options to degrees, you can use the SIN function to calculate the sine of an angle in degrees. Here’s an example:
=SIN(45)
This formula will return the sine of 45 degrees, which is approximately 0.707. You can use any angle in degrees as the input for the SIN function.
Real-World Applications of the SIN Function with Degrees

The SIN function, when used with degrees, has numerous practical applications in various fields. Here are a few examples:
Geography and Mapping
In geography and mapping, angles are often measured in degrees, minutes, and seconds. The SIN function can be used to calculate the sine of these angles for various calculations, such as determining the rise and run of a slope or finding the distance between two points on a map.
Architecture and Engineering
Architects and engineers frequently work with angles in degrees when designing structures. The SIN function can be used to calculate the sine of angles for roof pitches, ramp inclines, or the slope of a road, ensuring structural integrity and safety.
Physics and Mechanics
In physics and mechanics, the SIN function with degrees can be applied to calculate the displacement of objects in circular motion, analyze the behavior of springs, or determine the period of a pendulum.
Astronomy
Astronomers often use the SIN function with degrees to calculate the position of celestial bodies, determine the rise and set times of the Sun and Moon, or analyze the orbits of planets and satellites.
Advanced Uses of the SIN Function
The SIN function can be combined with other Excel functions and mathematical operations to perform more complex calculations. Here are a few advanced applications:
Combining with the COS Function
The COS function calculates the cosine of an angle. By combining the SIN and COS functions, you can perform calculations involving both sine and cosine, such as finding the horizontal and vertical components of a vector.
Using Array Formulas
Array formulas allow you to perform calculations on multiple cells simultaneously. You can use array formulas with the SIN function to calculate the sine of a range of angles, which can be useful for large datasets or when performing batch calculations.
Error Handling and Troubleshooting
It’s important to note that the SIN function returns an error if the input angle is not a numeric value or if it is out of the valid range of angles. Ensure that your input angles are within the range of -360 to 360 degrees, and always check for errors when using trigonometric functions.
| Angle (Degrees) | SIN Value |
|---|---|
| 0 | 0 |
| 30 | 0.5 |
| 45 | 0.707 |
| 60 | 0.866 |
| 90 | 1 |

Conclusion
The SIN function in Excel is a versatile tool that allows users to perform trigonometric calculations with angles in degrees. By understanding how to set the calculation options and use the SIN function effectively, you can apply it to a wide range of real-world scenarios and complex mathematical problems. Whether you’re working in geography, architecture, or physics, the SIN function is an invaluable asset for accurate and efficient calculations.
FAQ

What is the difference between using the SIN function with radians and degrees?
+The main difference is in the unit of measurement for angles. Radians are a unitless measure of angle, while degrees are a unit of measurement. When using the SIN function with radians, the input angle is interpreted as a radian value. When using it with degrees, the input angle is interpreted as a degree value. The SIN function calculates the sine of the angle, regardless of the unit, but the result may differ based on the input unit.
How accurate are the results of the SIN function in Excel?
+The SIN function in Excel is highly accurate for most practical purposes. It uses double-precision floating-point numbers, which provide a high level of precision. However, for extremely large angles or very precise calculations, there may be a small margin of error due to the limitations of floating-point arithmetic. In such cases, you might consider using specialized mathematical software or programming languages that offer greater precision.
Can I use the SIN function with angles outside the range of -360 to 360 degrees?
+Yes, you can use the SIN function with angles outside the range of -360 to 360 degrees. Excel wraps the angle to the nearest 360-degree interval. For example, the sine of 450 degrees is the same as the sine of 90 degrees, as both angles are in the same 360-degree interval. However, it’s important to keep in mind that the results may not be what you expect if you’re not familiar with the wrapping behavior of angles in trigonometry.



