How to Convert 3 3/4 to a Decimal

Converting fractions to decimals is a fundamental skill in mathematics, especially when dealing with measurements, financial calculations, and various real-world applications. In this guide, we will delve into the step-by-step process of converting the fraction 3 3/4 into its decimal equivalent. By understanding this conversion, we can enhance our numerical fluency and apply it to practical scenarios.
Understanding the Fraction 3 3⁄4
The fraction 3 3⁄4 represents a mixed number, which is a combination of a whole number and a proper fraction. In this case, we have 3 whole units and 3⁄4 of a unit. To convert this mixed number to a decimal, we need to break it down into its constituent parts and perform the necessary calculations.
Step-by-Step Conversion Process

Follow these systematic steps to convert 3 3⁄4 into a decimal:
- Separate the Whole Number and Fraction: Begin by identifying the whole number part, which is 3, and the fraction part, which is 3/4.
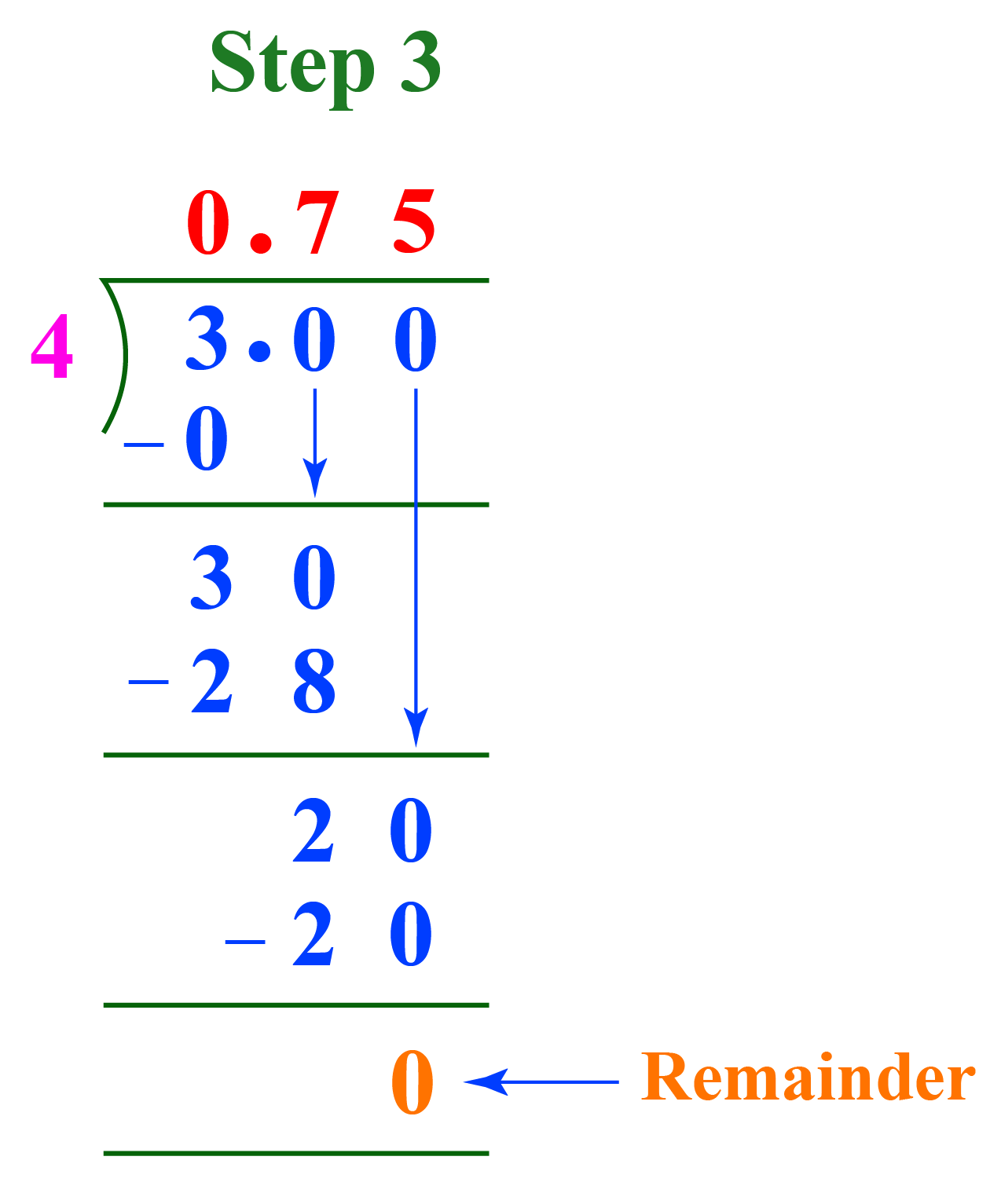
- Convert the Fraction to a Decimal: To convert 3/4 to a decimal, we can use the concept of division. Divide the numerator (3) by the denominator (4) to get the decimal equivalent. In this case, 3 divided by 4 equals 0.75.
- Combine the Whole Number and Decimal: Now, we have the whole number (3) and the decimal equivalent of the fraction (0.75). To express this as a single decimal, we simply add the two together: 3 + 0.75 = 3.75.
Therefore, the decimal representation of 3 3/4 is 3.75. This value represents the same quantity as the original mixed number, but in a decimal format.
Visualizing the Conversion
To gain a deeper understanding of the conversion process, let’s visualize 3 3⁄4 as a length on a number line. Imagine a number line extending from 0 to 4, with each unit representing 1⁄4 of the whole. The mixed number 3 3⁄4 would be positioned at 3 and 3⁄4 units along this number line. Converting this to a decimal involves dividing the fraction part (3⁄4) into equal segments and finding its decimal equivalent.
Real-World Applications
The ability to convert fractions to decimals is crucial in various practical situations. For instance, when measuring ingredients for a recipe, understanding decimal equivalents of fractions ensures precise measurements. In finance, converting fractions to decimals is essential for calculating interest rates, exchange rates, and stock prices. Additionally, in engineering and construction, decimal representations of fractions are used for accurate measurements and calculations.
Common Fraction-to-Decimal Conversions

Here are some common fraction-to-decimal conversions that are useful to know:
| Fraction | Decimal Equivalent |
|---|---|
| 1/2 | 0.5 |
| 1/4 | 0.25 |
| 3/8 | 0.375 |
| 5/16 | 0.3125 |
| 7/12 | 0.5833 (recurring) |
These conversions are valuable for quick references and can be applied to various mathematical problems and real-life scenarios.
Practical Exercises
To reinforce your understanding of fraction-to-decimal conversions, try these practical exercises:
- Convert 2 1/5 to a decimal.
- Express 5/8 as a decimal.
- Find the decimal equivalent of 1 3/10.
Remember to follow the step-by-step process and visualize the conversions to enhance your mathematical skills.
Conclusion
Converting fractions to decimals is a fundamental mathematical skill with practical applications in everyday life. By understanding the process and practicing with various fractions, you can become proficient in decimal conversions. This skill is not only useful for academic purposes but also for real-world scenarios, making it an essential tool for problem-solving and numerical fluency.
What is a mixed number in mathematics?
+A mixed number is a combination of a whole number and a proper fraction. It represents a value that consists of both whole units and a fractional part.
Can all fractions be converted to decimals?
+Yes, all fractions can be converted to decimals. The process involves dividing the numerator by the denominator to obtain the decimal equivalent. However, some decimal representations may have recurring digits.
Why is it important to convert fractions to decimals?
+Converting fractions to decimals allows for easier comparisons, calculations, and practical applications. It simplifies numerical representations and makes it more convenient to work with decimal values in various contexts.